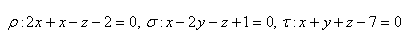Bod, priamka a rovina
1. Vysvetlite v akej vzájomnej polohe môže byť :
a) bod a rovina
b) priamka a rovina
Riešenie:
Bod a rovina.
Bod A[a1; a2; a3] leží v rovine ρ: a.x +by + cz +d = 0 ak jeho súradnice spĺňajú rovnicu roviny ρ .
Bod A[a1; a2; a3] neleží v rovine ρ: ax +by + cz +d = 0 ak jeho súradnice nespĺňajú rovnicu roviny ρ.
Vzdialenosť bodu A[a1; a2; a3] od roviny ρ: ax +by + cz +d = 0 určíme:
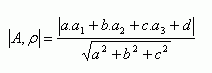
Priamka a rovina.

2.Ktorý z bodov A [3;2;7], B[0;2;1], C[-8;-2;-1] ležia v rovine τ : 2x – 3y – 2z+8 = 0. Aká musí byť hodnota x, aby bod M[x;-6;2] ležal tiež v danej rovine?
Riešenie:
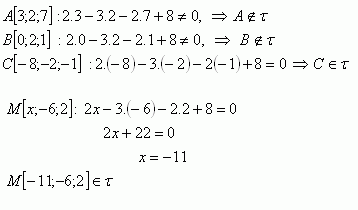
V rovine τ ležia body C [-8;-2;-1] a M [-11;-6;2].
3. Zistite či bod A[9;-2;0] leží v rovine ξ: 3x + 2y – 6z +26 = 0. Ak neleží, vypočítajte jeho vzdialenosť od danej roviny.
Riešenie:
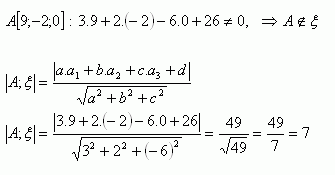
Bod A neleží v rovine ξ . Jeho vzdialenosť od tejto roviny je 7 jednotiek.
4.Vypočítajte vzdialenosť začiatku súradnicovej sústavy od roviny:
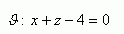
5.Určite vzájomnú polohu rovín ρ a τ. Ak sú rovnobežné rôzne, určite aj ich vzdialenosť. Rovnice rovín sú:

6.Čo musí platiť pre súradnicu y bodu A [1;y;0], aby jeho vzdialenosť od roviny τ: 3x – 2y – 6z = 0 bola 5j.
Prihláste sa pre zobrazenie riešenia
7. Ziastite vzájomnú polohu a priesečník priamky a roviny, ak sú navzájom rôznobežné.
τ: x +y + z +1
Priamka:
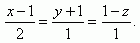
8. Daná je priamka p a rovina ρ . Zistite ich spoločný bod a odchylku priamky od roviny. Ich rovnice sú:
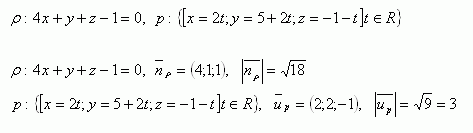
9.Určite vzájomnú polohu rovín ρ a π , ktorých rovnice sú:
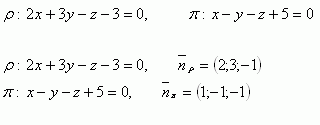
10.Vypočítajte uhol dvoch rôznobežných rovín:
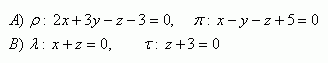
11.Určite spoločný bod priamky p a roviny τ ak platí:
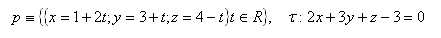
12.Vzdialenosť bodu A od roviny σ predstavuje stranu štvorca ABCD. Vypočítajte obsah tohto štvorca ak platí:
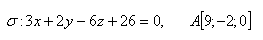
13.Vypočítajte vzdialenosť dvoch rovnobežných rovín σ a τ ak platí:
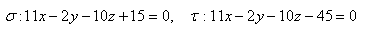
14.Vypočítajte dĺžku výšky zostrojenej z vrchola V v štvorstena ABCV, ak platí:
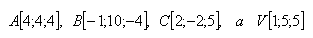
15.Určite reálne čísla a, b, aby roviny π a τ boli rovnobežné, ak platí:
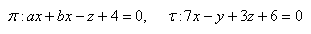
16.Určite vzájomnú polohu rovín σ a η ak platí:
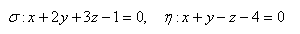
17.Ukážte, že súradnicové roviny xy a yz sú navzájom kolmé.
Prihláste sa pre zobrazenie riešenia18.Určite uhol priamky p s rovinou μ ak platí:
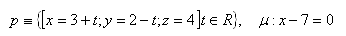
19.Vrcholy štvorstena sú body A,B,C,D. Určite odchýlku hrany AD od roviny ρ = ABC ak platí:
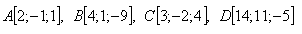
20.Určite vzájomnú polohu troch rovín ak platí: