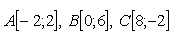Vektor v rovine
1. Charakterizujte vlastnosti vektora v rovine:

2. Dané sú body A[-2;5], B[1;yB] a C[4;-3].
a) vektory AB a AC sú kolmé
b) vektory AB a AC sú rovnobežné
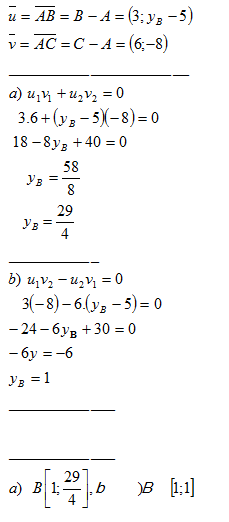
3. Daný je vektor v = AB takto: A[1;1], B[b1;b2] a stred vektora S[4;5].
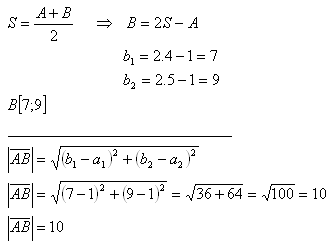
Bod B má súradnice B[7;9]. Veľkosť vektora je 10 jednotiek.
4. Dané sú body A[2;-3] a B[x;0].
5. Dokážte, že trojuholník, ktorého vrcholy sú body A[-3;-2], B[1;4] a C[-5;0] je rovnoramenný.
Prihláste sa pre zobrazenie riešenia6. Dané sú vektory a = (3;-2) a b = (-1;5).
a.c = 17
b.c = 3
7. Nájdite vektor v, kolmý na vektor u = (3;4) a ktorého veľkosť je 15.
Prihláste sa pre zobrazenie riešenia8. Vrcholy trojuholníka ΔABC tvoria body A[1;1], B[2;-1] a C[3;2].
9. Na súradnicových osiach nájdite bod, ktorý má od bodu A [4;-6] vzdialenosť 5.
Prihláste sa pre zobrazenie riešenia10.Vrcholy štvoruholníka sú v bodoch: A[0;0], B[3;-4], C[6;0] a D[3;4].
11.Body A, B, C sú vrcholy trojuholníka ABC. Ukážte, že trojuholník ABC je rovnostranný. Vypočítajte jeho obsah.
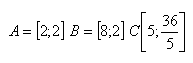
12. Body A, B, C sú vrcholy trojuholníka ABC. Stredy strán AC, BC označte M,N. Ukážte, že stredná priečka MN je rovnobežná so stranou AB a že platí MN = 0,5AB.
13. Daný je rovnoramenný lichobežník ABCD s vrcholmi
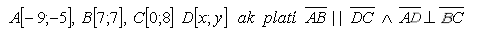
Určite súradnice bodu D.
14.Určite súradnice stredu S a veľkosť polomeru r kružnice, ktorá prechádza bodmi A,B,C. Riešte pre body:
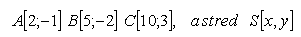
15. Nájdite súradnice ťažiska sústavy štyroch rovnako hmotných telies, ktoré ležia v bodoch A,B,C,D. Ťažisko T je stred úsečky, ktorej koncové body sú v strede vektorov
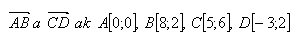
16.Bod A [2;5] je začiatok sily F, ktorej priemet na súradnicové osi je x = 3; y = 3. Vypočítajte koniec vektora, ktorý zobrazuje silu F.
17. Dané sú tri body A,B,C
- a.) Dokážte, že ležia na jednej priamke
- b.) Zistite v akom pomere sú veľkosti vektorov
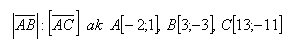
18. Rovnoramenný trojuholník ABC má základňu AB s vrcholom A a stredom základne S. Jeho vrchol C leží na osi x. Určite vrcholy trojuholníka B a C.
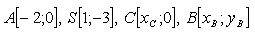
19. Je daný vektor u = (5 ;-3) a taký vektor v = (1;yv) že platí
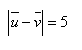
Určite yv
20. Body A,B,C sú vrcholy trojuholníka ABC a body M,N,P sú stredy strán tohto trojuholníka. Určite súradnice troch vektorov, ktorých umiestnenie splýva s ťažnicami trojuholníka ABC tak, že začiatočný bod je vždy vo vrchole trojuholníka. Vypočítajte veľkosti týchto vektorov.