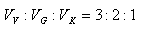Dôkazy
1. Ako dokazujeme pravdivosť matematickej vety?
Riešenie:

2.Priamym dôkazom dokážte vetu:
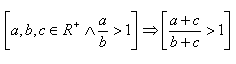
Riešenie:
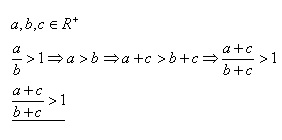
Čo platí podľa predpokladu.
3.Priamym dôkazom dokážte vetu:
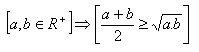
Riešenie:
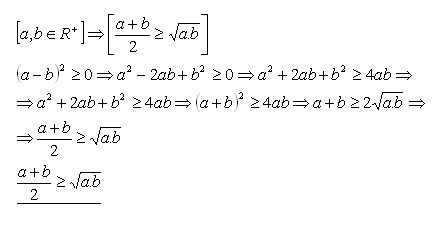
Platí pre všetky a,b z R+
4.Priamym dôkazom dokážte vetu:
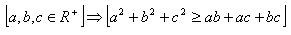
5.Priamym dôkazom dokážte vetu:
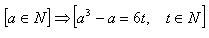
6.Nepriamym dôkazom dokážte vetu: Ak a2 je prirodzené číslo deliteľná 3, potom aj a je prirodzené číslo deliteľná 3.
Prihláste sa pre zobrazenie riešenia
7.Nepriamym dôkazom dokážte vetu: pre prirodzené číslo a platí: Ak a4 + 2 nie je deliteľné 3, potom a je deliteľné 3.
Prihláste sa pre zobrazenie riešenia
8.Dokážte sporom vetu: Pre všetky kladné reálne čísla a, b platí:
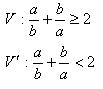
9.Dokážte sporom vetu : Číslo √3 je iracionálne
Prihláste sa pre zobrazenie riešenia
10. Matematickou indukciou dokážte vetu: Pre všetky prirodzené čísla n platí:
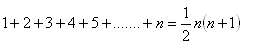
11.Matematickou indukciou dokážte vetu: Pre všetky prirodzené čísla n platí:
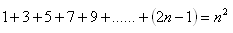
12.Matematickou indukciou dokážte vetu: Pre každé prirodzené číslo n platí:
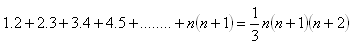
13. Matematickou indukciou dokážte vetu: Pre každé prirodzené číslo n platí:
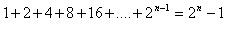
14.Matematickou indukciou dokážte vetu:
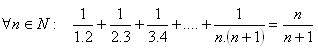
15.Matematickou indukciou dokážte vetu:
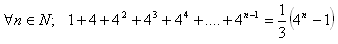
16.Matematickou indukciou dokážte Moivreovu vetu
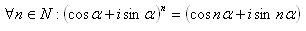
17.Vo vnútri trojuholníka Δ ABC je daný bod U. Dokážte, že platí vzťah
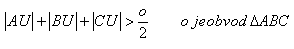
18.Dokážte vetu: Ťažnica trojuholníka je menšia ako polovica obvodu.
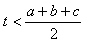
19.Dokážte vetu:
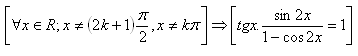
20.Rovnostrannému valcu je vpísaná guľa a kužeľ. Podstava kužeľa je zhodná s podstavou valca, vrchol kužeľa je v strede druhej podstavy. Ukážte, že Archimedova úloha platí. (Archimedes asi 287–212 pred n. l.)