Pravdepodobnosť
1. Definujte a charakterizujte pravdepodobnosť.
a) Klasická definícia pravdepodobnosti
Nech náhodný pokus spĺňa predpoklady
- počet všetkých výsledkov je konečný
- všetky výsledky sú rovnako možné
- žiadne dva výsledky nemôžu nastať súčasne
Pravdepodobnosť javu A je číslo
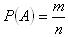 , kde n je počet všetkých možných výsledkov náhodného pokusu a m je počet všetkých priaznivých výsledkov, t.j. výsledkov, pri ktorých nastane jav A.
, kde n je počet všetkých možných výsledkov náhodného pokusu a m je počet všetkých priaznivých výsledkov, t.j. výsledkov, pri ktorých nastane jav A. Platí : 0 ≤ P(A) ≤ 1
Pravdepodobnosť nemožného javu : P(A) = 0
Pravdepodobnosť istého javu: P(A) = 1
b) Podmienená pravdepodobnosť udalosti A za podmienky B je číslo:
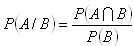
c) Pravdepodobnosť nezávislých javov:
P(A∩B) = P(A)P(B)
d) Pravdepodobnosť nezlučiteľných javov:
P(AUB) = P(A) + P(B)
e) Binomické rozdelenie pravdepodobnosti:
Nech A je jav s pravdepodobnosťou P. Potom pravdepodobnosť, že pri n-násobnom opakovaní pokusu, jav A nastane práve k- krát je číslo:
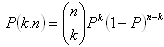
f) Hypergeometrické rozdelenie pravdepodobnosti.
Nech V predmetov vybraných z N predmetov má určitú vlastnosť, potom N-V predmetov túto vlastnosť nemá.
Pravdepodobnosť, že práve k predmetov spomedzi n náhodne vybraných predmetov túto vlastnosť má, je číslo:
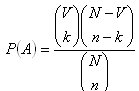
2. Z osemnástich lístkov očíslovaných 1 - 18 vytiahneme náhodne jeden lístok. Aká je pravdepodobnosť, že na vytiahnutom lístku bude:
b) číslo deliteľné 3
c) prvočíslo
d) deliteľné 6
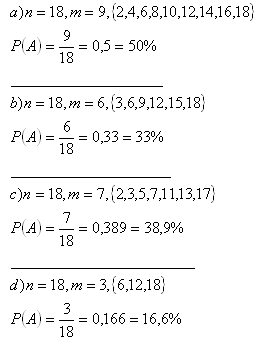
3. Aká je pravdepodobnosť že pri hode dvoma kockami (červenej a modrej) padne:
b) súčet, ktorý je deliteľný piatimi
c) súčet, ktorý bude párny
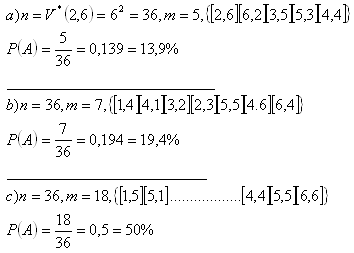
4. Hazardný hráč hádžuci tromi kockami, položil G. Galileiovi otázku : „Mám staviť na súčet 11 alebo súčet 12?“ Čo mu Galilei odpovedal?
Prihláste sa pre zobrazenie riešenia5. Dlhodobé výskumy na istom území ukázali, že zo 100 000 detí sa 82 170 dožije 40 rokov a 37 930 sa dožije 70 rokov. Aká je pravdepodobnosť, že človek, ktorý sa dožije 40 rokov, dožije sa aj 70 rokov?
Prihláste sa pre zobrazenie riešenia6. V meste sú štyri križovatky so svetelnými semafórmi. Každý z nich uvoľňuje alebo uzatvára dopravu s rovnakou pravdepodobnosťou 0,5. Aká je pravdepodobnosť, že auto:
b) prejde prvými dvomi križovatkami bez zdržania
c) prejde všetkými štyrmi križovatkami bez zdržania
7. V 32 hracích kartách sú 4 esá a 12 figúr (4 králi, 4 horníci a 4 dolníci). Aká je pravdepodobnosť, že náhodne vytiahnutá jedna karta bude eso alebo figúra?
Prihláste sa pre zobrazenie riešenia8. Otcovia sú šťastní, keď sa im narodí syn. Z dlhodobých štatistík je známe, že pravdepodobnosť narodenia chlapca je P(A) = 0,51.
9. V šestnástich fľašiach sú minerálky. Vieme, že v 10 fľašiach je Slatina a v 6 fľašiach je Baldovská. Aká je pravdepodobnosť, že medzi 4 náhodne vybratými fľašami sú 2 Slatiny a 2 Baldovaké?
Prihláste sa pre zobrazenie riešenia10. V hazardnej číselnej hre sa losuje 6 čísiel zo 49 čísiel. Aká je pravdepodobnosť získať:
b) tretie poradie
c) druhé poradie
d) prvé poradie