Kruh
1. Charakterizujte kruh a jeho časti:
- kruh
- kruhový výsek
- kruhový odsek
- medzikružie
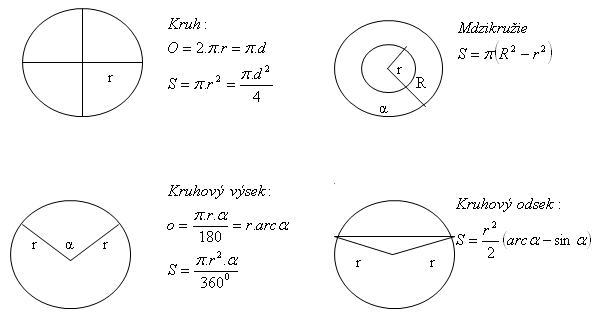
2. Stredná dvoch kružníc, ktoré sa dotýkajú zvonka je 12 cm a súčet obsahov obidvoch kruhov je 80π cm2.
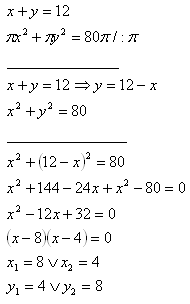
Polomery kružníc sú r1 = 8 cm, r2 = 4 cm.
3. Kruh s polomerom R = 28 cm rozdeľte sústrednou kružnicou tak, aby obsahy vzniknutých častí boli rovnaké.
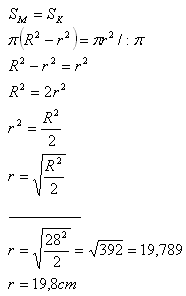
Polomer menšej sústrednej kružnice je r = 19,8 cm.
4. Vypočítajte polomer kružnice, ak je daná dĺžka jej tetivy t = 16 cm a výška príslušného kruhového odseku v = 5 cm.
5. Kruh s polomerom R je rozdelený sústrednou kružnicou s polomerom r. Pomer obsahu vnútorného kruhu ku obsahu medzikružia je rovnaký ako pomer obsahu medzikružia ku obsahu vonkajšieho kruhu.
6. Tri rovnaké kružnice (r = 8 cm) sa navzájom dotýkajú.
7. Rovnoramenný trojuholník má a =10 cm, b = c = 13cm. Do trojuholníka je vpísaná kružnica.
8. Výška kruhového odseku je 2 cm, stredový uhol α = 60°.
9. Okolo kruhového záhona je cestička široká 40 cm. Záhon má priemer 3m a 20cm.
10. Prvé koleso súkolesia ozubených kolies má 60 zubov. Druhé koleso zapadajúce do prvého kolesa má 42 zubov. Tretie koleso zapadajúce do druhého kolesa má 15 zubov. Prvé koleso sa otočí sedemkrát.