Pravouhlý trojuholník
1. Definujte pravouhlý trojuholník.
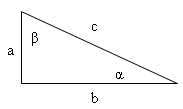
a) Pytagorova veta:
a2 + b2 = c2
b) Goniometrické funkcie:
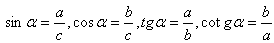
c) Obvod trojuholníka:
O = a + b + c
d) Obsah trojuholníka:
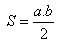
c) Euklidove vety:
a2 = c.ca
b2 = c.cb
v2 = ca.cb
2. V pravouhlom trojuholníku ΔABC sú dané odvesny a =3 cm, b = 4 cm.
a) preponu c
b) výšku na preponu vc
c) obsah trojuholníka S
d) ostré uhly α a β
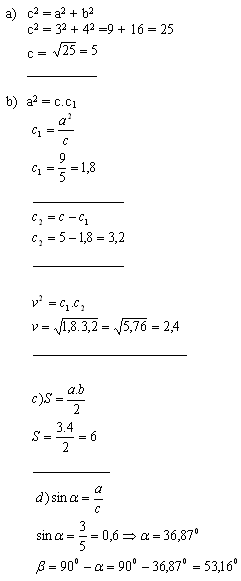
V trojuholníku ΔABC platí: c = 5cm, vc = 2,4cm, S = 6cm2, α = 36,87°, β = 53,16°.
3. V pravouhlom trojuholníku sú a, b odvesny, c prepona, α je uhol proti odvesne a.
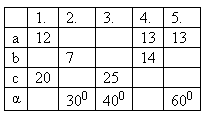

4. Strany pravouhlého trojuholníka tvoria aritmetickú postupnosť. Vypočítajte:
b) jeho obsah
ak veľkosť dlhšej odvesny je 16 cm.
5. Určite obvod pravouhlého trojuholníka, ak súčet jeho odvesien je 30 cm a jeho obsah je 110,5 cm2.
Prihláste sa pre zobrazenie riešenia6. Vypočítajte veľkosť základne a ramena rovnoramenného trojuholníka, ak rameno je o 1 cm dlhšie ako základňa a výška na základňu je o 2 cm kratšia ako rameno.
Prihláste sa pre zobrazenie riešenia7. Dokážte, že ak trojuholník má strany a = 4p2- 1, b = 4p, c = 4p2+1 je pravouhlý a volá sa Pytagorejský trojuholník. Napíšte štyri takéto trojuholníky.
Prihláste sa pre zobrazenie riešenia8. Aké stúpanie má cesta, ak na dopravnej značke, ktorá o tom informuje, je napísané 6,7 %? Auto prešlo 2,3 km po tejto ceste.
9. Vypočítajte obsah rovnoramenného pravouhlého trojuholníka, ktorého obvod je 20cm.
Prihláste sa pre zobrazenie riešenia10. Pre odvesny pravouhlého trojuholníka platí a:b = 2:3. Prepona má dĺžku 10 cm.