Atomový obal
1.Jak vypadá atom?
Řešení:
Aristotelés (384 př. n. l.): Hmota je spojitá, dá se dělit do nekonečna. Leukippos, Démokritos (5. stol. př. n. l.): Hmota je nespojitá, skládá se z dále nedělitelných částic – atomů. J. J. Thomson (1856–1940) vytvořil tzv. model „rozinkového koláče“. Atom je kladně nabitá koule, v níž se vznášejí elektrony. E. Rutherford (1871–1937) vytvořil „planetární model atomu“. Celá hmotnost atomu (a také jeho kladný náboj) je soustředěna v jádře (10–15 m). Kolem jádra po kružnici (elipse – A. Sommerfeld) obíhají elektrony. Poloměr atomu je asi 10–10 m. Hlavním nedostatkem tohoto modelu bylo, že při obíhání elektronu kolem jádra by elektron ztrácel energii, jeho rychlost by se zmenšovala, pohyboval by se po spirále a spadl by na jádro. Hmotný svět by nemohl existovat. N. Bohr (1883–1962) vytvořil „kvantový model atomu“.
- a.) Elektron se může pohybovat kolem jádra jen po zcela určitých kruhových drahách, které se nazývají orbitaly (energetické hladiny). Délka orbitalu se rovná celočíselnému násobku vlnové délky de Broglieovy vlny příslušející elektronu.
- b.) Když se elektron pohybuje po orbitalu, nevyzařuje energii.
- c.) Při přechodu elektronu z jednoho orbitalu, na němž měl energii En, na jiný orbital s menší energií Em vyzáří jedno světelné kvantum – foton. W. Heisenberg (1901–1976), E. Schrödinger (1887–1961) vytvořili „kvantově-mechanický, pravděpodobnostní model“. Není možné stejně přesně určit polohu elektronu a současně jeho rychlost. Lze určit místa, kde se může elektron s určitou pravděpodobností v prostoru kolem jádra nacházet.
2.Jaké vlastnosti má atom vodíku v Bohrově modelu?
Řešení:

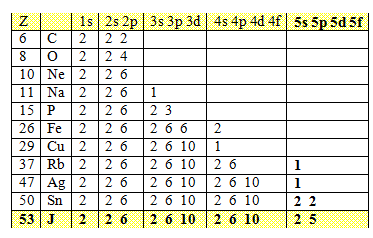
Obsazení drah elektronového obalu některých atomů:
3.Za jaký čas proletí světlo atomem s poloměrem r = 3.10–10 m
Řešení:
Rozbor:
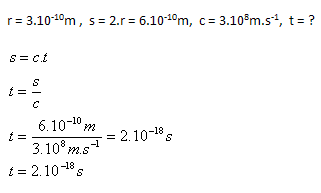
Světlo proletí atomem za čas t = 2.10–18 s.
4.Vypočítejte energii základního stavu atomu vodíku E1. 1 J = 0,6242.1019 eV
Pro zobrazení řešení se přihlaste.
5.Vypočítejte energie atomu vodíku na stacionárních drahách s hlavním kvantovým číslem n = 1,2,3,4,5,6. Energie na první kvantové dráze je E1 = −13,6 eV. (příklad 4)
Pro zobrazení řešení se přihlaste.
6.Vypočítejte rychlosti pohybu elektronu na jednotlivých orbitalech v atomu vodíku, když víte, že
r1 = 0,53.10–10 m.
Pro zobrazení řešení se přihlaste.
7.Určete frekvenci viditelných čar Balmerovy série (J. Balmer, 1825–1898) pro vodík. Série vznikne přeskoky elektronů na druhou kvantovou dráhu.
Pro zobrazení řešení se přihlaste.
8.Atom vodíku, který je v základním stavu, získal energii 10,2 eV. Na kterou energetickou hladinu při tom přešel elektron?
Pro zobrazení řešení se přihlaste.
9.Heliově–neonový laser má výkon 2 mW a vysílá záření vlnové délky 632,8 nm. Určete energii, hmotnost a hybnost emitovaných fotonů.
Pro zobrazení řešení se přihlaste.
10.Atom vodíku přejde ze stacionárního stavu n = 6 do stavu m = 1. Vypočítejte frekvenci a vlnovou délku vyzářeného fotonu. Použijte Rydbergův zákon. (J. R. Rydberg 1854–1919)
Pro zobrazení řešení se přihlaste.
11.Vypočítejte velikost elektromagnetické energie, kterou vyzáří atom vodíku, když jeho elektron přeskočí z prvního orbitalu na nekonečně vzdálený orbital.
Pro zobrazení řešení se přihlaste.
12.Odvoďte Rydbergovu konstantu R
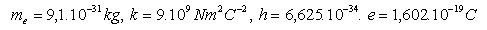
13.Určete tři nejdelší vlnové délky Balmerovy série. Tato série odpovídá vyzařování energie elektronu při přechodech 3 – 2, 4 – 2, 5 – 2.
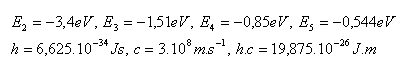
14.Jaké napětí musí být v elektrickém poli, máme-li v něm urychlit elektron tak, aby mohl při srážce s atomem vodíku převést atom ze základního stavu do prvního excitovaného stavu.
Pro zobrazení řešení se přihlaste.
15.Poloměr první kruhové dráhy elektronu v atomu vodíku je r = 0,53.10–10 m. Určete intenzitu elektrického pole od jádra na této dráze.
Pro zobrazení řešení se přihlaste.
16.Jak velký je potenciál jádra atomu na první dráze elektronu v atomu vodíku?
(E = 51,3.1010 N.C–1 – příklad 15)
Pro zobrazení řešení se přihlaste.17.Zjistěte, zda může nastat fotoelektrický jev při dopadu viditelného světla na zinek WV(Zn) = 4 eV. Nejkratší vlnová délka viditelného světla je λ = 390 nm.
Pro zobrazení řešení se přihlaste.
18.Výstupní práce z platiny je WV(Pt) = 5,29 eV. Vypočítejte mezní kmitočet f0, při kterém nastane fotoelektrický jev.
Pro zobrazení řešení se přihlaste.
19.Jakou rychlostí vystupují elektrony z povrchu cézia, když jeho povrch osvítíme monochromatickým světlem s vlnovou délkou λ = 590 nm. Výstupní práce cézia je WV(Cs) = 1,93 eV
Pro zobrazení řešení se přihlaste.
20.Odvoďte vztah pro výpočet energie elektronu, který je vázán na úsečku délky L.
Pro zobrazení řešení se přihlaste.
21.Jaká bude energie základního a prvního excitovaného stavu elektronu vázaného na úsečku L = 4.10–10 m
Pro zobrazení řešení se přihlaste.
22.Jakou délku musí mít úsečka, na kterou je vázán elektron, aby rozdíl energií základního a prvního excitovaného stavu byl menší než 3 eV.
Pro zobrazení řešení se přihlaste.
23.Jakou elektronovou konfiguraci má atom sodíku, železa, mědi a stříbra? Použijte tabulku v příkladu č. 2.
Pro zobrazení řešení se přihlaste.
24.Které prvky mají dané konfigurace:
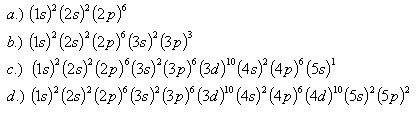
25.Určete energii elektronu v základním stavu molekuly butadiénu s konfigurací (1s)2(2s)2. Elektrony se pohybují po celé délce L = 0,6.10–9 m molekuly.
Pro zobrazení řešení se přihlaste.