Odraz a lom světla
1. Co se stane, když světlo prochází rozhraním dvou prostředí?
Řešení:
Když světlo prochází rozhraním dvou prostředí z prvního prostředí (kde se pohybuje rychlostí v1) do druhého prostředí (kde se pohybuje rychlostí v2), mohou nastat dva případy:
- odraz světla (reflexe)
- lom světla

2.Rychlost červeného světla ve skle je v1 = 199 200 km·s–1 a fialového v2 = 196 700 km·s–1. Určete index lomu pro červené a fialové světlo. (c = 3·108 m·s–1)
Řešení:
Rozbor:
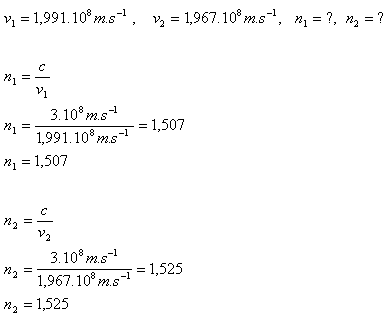
Index lomu pro červené světlo ve skle je n1 = 1,507, pro fialové je n2 = 1,525.
3.Světlo dopadá ze vzduchu (n1 = 1) na stěnu diamantu pod úhlem α = 68°. Lomený paprsek je kolmý na odražený paprsek. Vypočítejte“
- index lomu diamantu pro použité světlo
- rychlost světla v diamantu (c = 3·108 m·s–1)
Řešení:
Rozbor:
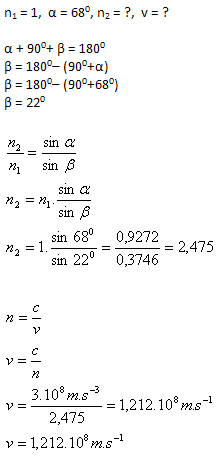
- Index lomu diamantu je n2 = 2,475.
- Rychlost světla v diamantu je v = 1,212·108 m·s–1.
4.Světlo dopadající ze vzduchu na vodní hladinu (n = 1,33) se láme pod úhlem β = 30°. Určete úhel dopadu α a úhel odrazu α‘.
Pro zobrazení řešení se přihlaste.
5.Na dně jezera je zasazen ve svislé poloze sloup 1 metr dlouhý tak, že je celý ponořen pod hladinou vody. Určete délku jeho stínu na dně jezera, pokud n1 (vzduch) = 1, n2 (voda) = 1,33 a Slunce je φ = 30° nad hladinou.
Pro zobrazení řešení se přihlaste.
6.Světelný paprsek dopadá ze vzduchu na rovinné rozhraní vzduchu a skla, odráží se pod úhlem 60° a zároveň se láme do skla pod úhlem 30°. Určete rychlost světla ve skle.
Pro zobrazení řešení se přihlaste.
7.Vlnová délka žlutého světla ve vzduchu je λ0 = 590 nm. Jaká bude vlnová délka světla ve skle při n = 1,5? Vypočítejte také rychlost světla v tomto prostředí.
Pro zobrazení řešení se přihlaste.
8.Pod jakým mezním úhlem musí dopadat světlo, aby nastal totální odraz, pokud světlo přechází:
- a) ze skla do vzduchu (n1 = 1,5)
- b) z vody do vzduchu (n‘1 = 1,33)
- c) ze skla do vody n2 (vzduch) = 1
9. Určete tloušťku stěny mýdlové bubliny (n = 1,33), pokud na ni dopadá bílé světlo. Interferenční maximum prvního řádu pozorujeme v zelené barvě (fZ = 5,7·1014 Hz).
Pro zobrazení řešení se přihlaste.10.Na dně potoka hlubokého 32 cm leží kamínek. Chlapec se jej chce dotknout holí, kterou drží nad hladinou pod úhlem 45°. V jaké vzdálenosti od kamínku se po ponoření hole dotkne dna potoka? (n1 = 1, n2 = 1,33)
Pro zobrazení řešení se přihlaste.
11. Index ledu je n1 = 1,31, skla n2 = 1,51, oleje n3 = 1,47. Jaká je rychlost světla v těchto prostředích?
Pro zobrazení řešení se přihlaste.12. Vypočítejte index lomu látky, jestliže při úhlu dopadu α = 30° ze vzduchu je úhel lomu β = 15°. Jaký musí být úhel dopadu α/, je-li úhel lomu β/ = 21,5°?
Pro zobrazení řešení se přihlaste.13.Na rovinné zrcadlo dopadá světelný paprsek pod úhlem dopadu α = 20°. Jak se změní úhel mezi dopadajícím a odraženým paprskem, bude-li paprsek dopadat na zrcadlo pod úhlem α/ = 35°
Pro zobrazení řešení se přihlaste.14.Světelný paprsek přechází z vody (n1 = 1,33) do skla (n2 = 1,51). Rozhodněte, zda jde o lom ke kolmici, nebo o lom od kolmice, je-li úhel dopadu α = 60°.
Pro zobrazení řešení se přihlaste.15. O jak velký úhel se otočilo zrcátko, jestliže se na stupnici, jejíž vzdálenost od zrcadla je l = 150 cm, posune světelný paprsek z nulové polohy, při níž dopadá kolmo na stupnici, o h = 25 cm.
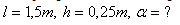
16.Na zrcadlo dopadá světelný paprsek. Zrcadlo se otočí o 1° kolem osy ležící v rovině zrcadla a kolmé na paprsek. O jaký úhel se odkloní odražený paprsek? O kolik se posune světelná stopa na stínidle, které je kolmé na odražený paprsek a vzdálené 5 m od zrcadla?
Pro zobrazení řešení se přihlaste.17. Jaký je mezní úhel při dopadu světla na rozhraní skla (n1 = 1,51) a vody (n2 = 1,33)?
Pro zobrazení řešení se přihlaste.18.Ve vodě v hloubce h = 600 mm pod hladinou je umístěn bodový zdroj světla. Určete tvar a rozměr té části povrchu vody, kterou světlo vystupuje nad vodní hladinu.
Pro zobrazení řešení se přihlaste.19.Lomený paprsek svírá s odraženým paprskem úhel ω = 90°. Určete relativní index lomu látky, do které se paprsek láme, platí-li sin α = 0,8.
Pro zobrazení řešení se přihlaste.20. Světelný paprsek dopadá ze vzduchu (n = 1) na sklo pod úhlem α = 60°. Index lomu skla pro červené světlo je n1 = 1,735, pro fialové n2 = 1,811. Určete úhel mezi lomeným červeným a fialovým paprskem.
Pro zobrazení řešení se přihlaste.