Extrémy - slovní úlohy
1.Číslo 32 rozložte na dvou sčítanců tak, aby jejich součin byl největší.
Řešení:
První sčítanec : x x = 16
Druhý sčítanec : 32 – x 32 – 16=16
y = x.(32 – x)
y = 32x – x2
y‘ = 32 – 2x
32 – 2x = 0
2x = 32
x =16
y‘‘ = -2 < 0 - maximum
První sčítanec je 16, druhý také 16
2.
Číslo 16 rozložte na dvou sčítanců tak, aby součet druhých mocnin těchto sčítanců byl nejmenší.
Řešení:
První sčítanec : x x = 8
Druhý sčítanec : 16 – x 16 – 8 = 8
y = x2 + ( 16 – x )2
y = x2 + 256 -32x +x2
y = 2x2 – 32x + 256
y‘ = 4x – 32
4x - 32 = 0
4x = 32
x = 8
y‘‘ = 4 > 0 - minimum
První sčítanec je 8, druhý také 8
3.Najděte takové kladné číslo x, aby součet tohoto čísla a jeho převrácené hodnoty byl nejmenší.
Řešení:
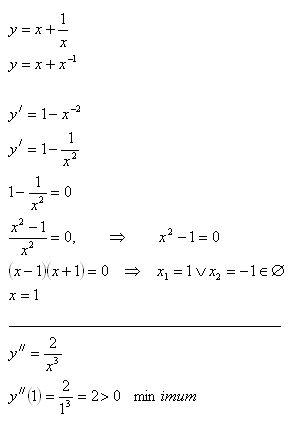
Hledané číslo je x = 1.
4.Z drátu délky l = 120 cm máme udělat model kvádru se čtvercovou podstavou. Jaké má mít rozměry, aby povrch byl maximální?
Pro zobrazení řešení se přihlaste.
5. Zahrada tvaru obdélníku má obvod 200 m. Určitě rozměry zahrady tak, aby její obsah byl maximální.
Pro zobrazení řešení se přihlaste.
6.Kdy má kvádr o objemu V = 63 cm3 a výškou v = 7 cm nejmenší povrch?
Pro zobrazení řešení se přihlaste.
7.
Na břehu řeky třeba oplotit zahradu obdélníkového tvaru (jednu stranu obdélníku tvoří řeka) pletivem dlouhým l = 800 m. Jaké rozměry musí mít zahrada, aby jí výměra byla maximální?
Pro zobrazení řešení se přihlaste.
8.Jaké jsou rozměry otevřeného bazénu se čtvercovým dnem, pokud bazén má objem V = 32 m3 a pokud na jeho vyzdění má spotřebovat minimální množství materiálu.
Pro zobrazení řešení se přihlaste.
9. Drát s délkou 5 m ohněte do pravého úhlu tak, aby vzdálenost obou konců byla minimální. Kde je třeba drát ohnout?
Pro zobrazení řešení se přihlaste.
10. Z plechu tvaru čtverce o straně 30 cm třeba v rozích vystřihnout čtyři stejné čtverečky, zbytek přehnout tak, aby vznikla otevřená krabice. Určitě stranu odstřižených čtverečků x tak, aby objem krabice byl maximální.
Pro zobrazení řešení se přihlaste.
11.Jáma s objemem 500 m3 má tvar kvádru se čtvercovou podstavou se stranou xa hloubkou h. Při jakých rozměrech x a h bude mít jáma minimální povrch?
Pro zobrazení řešení se přihlaste.12.Daná je parabola y = 4 - x2. Najděte vrcholy obdélníku ABCD s největším obvodem, jehož vrcholy A, B leží na ose x, vrcholy C, D mají kladné y-ové souřadnice a leží na parabole.
Pro zobrazení řešení se přihlaste.
13.Určete rozměry (r, v) válcové nádoby bez víka, jejíž povrch je S = 27π tak, aby její objem byl největší.
Pro zobrazení řešení se přihlaste.14.Nahoru otevřená nádoba tvaru válce má objem V = 3140 cm3. Určete rozměry válce (r, v) tak, aby na vytvoření této nádoby se minulo nejméně materiálu.
Pro zobrazení řešení se přihlaste.15. Jaké rozměry musí mít obdélník s obvodem O = 40cm, aby jeho úhlopříčka byla minimální.
Pro zobrazení řešení se přihlaste.