Determinant
1. Co je determinant a jaké má vlastnosti?
Řešení:
Determinant n - tého řádu je číslo D, vytvořené z n2 čísiel aik, uspořádaných do čtvercové tabulky n řádků a n sloupců tvaru

a11,a12,...a1n =>řádek determinatu
a11,a21,...an1 =>sloupec determinatu
a11,a22,...ann =>hlavní diagonála
Hodnota determinantu:
- Determinant druhého řádu
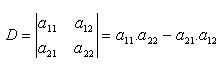
- Determinant třetího řádu (Sarrusovo pravidlo)
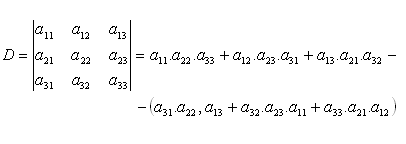
Determinant n-tého stupně:
Determinant n-tého stupně má n řádků a n sloupců. (n>3) Subdeterminant (minor) Mij příslušný k prvku aij vznikne z determinantu D vynecháním i-tého řádku a j-tého sloupce.
Algebraický doplněk (kofaktor):
Aij =(-1)i+j.aij.Mij
Rozvoj determinantu:
a.) dle i-tého riadku:
D=ai1Mi1 + ai2Mi2 + ... + ainMin
b.) dle j-tého stĺpca:
D=a1jM1j + a2jM2j + ... + anjMnj
2. Vyslovte věty o hodnotě determinantu
Řešení:
- 1) Hodnota determinantu se nezmění, pokud v něm zaměníme řádky za sloupce.
- 2) Hodnota determinantu se nezmění, pokud k libovolnému řádku přičteme (odečítáme) libovolný násobek ostatních řádků.
- 3) Hodnota determinantu se rovná nule, jsou-li v některém řádku všechny prvky rovné nule.
- 4) Hodnota determinantu se rovná nule, pokud některý řádek je libovolným násobkem jiného řádku.
- 5) Hodnota determinantu se rovná nule, pokud má dva řádky stejné.
- 6) Determinant změní znaménko, pokud mezi sebou vyměníme dva řádky determinantu.
- 7) Před determinant můžeme vybrat číslo "c", kterým je vynásoben některý řádek.
- 8) násobeny determinant číslem "c", znamená vynásobit tímto číslem některý jeho řádek. (Pouze jediný řádek) c <> 0
Poznámka:
Uvedené vlastnosti platí také pro sloupce determinantu.
3.Vyčíslete determinanty:
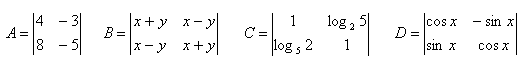
Řešení:
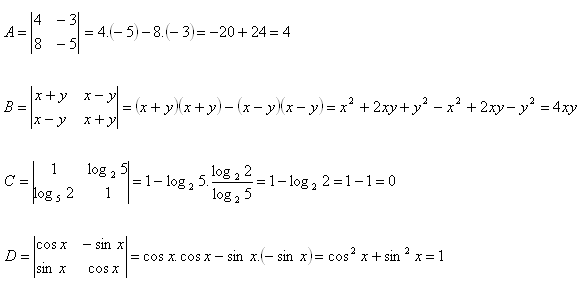
4.Vyčíslite determinanty:
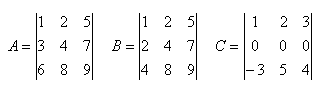
5.Vyčíslete determinanty:
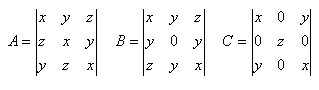
6. V množině R řešte rovnice:
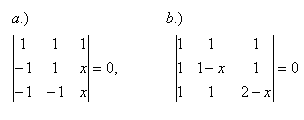
7.V množině R řešte rovnice:
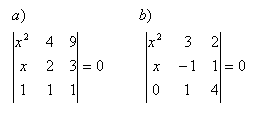
8.Vypočítejte obsah trojúhelníku ABC, který má vrcholy:
9. Vypočítajte obsah trojuholníka ABC, ktorého strany majú rovnice:
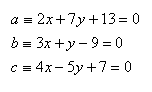
10.Zjistěte, zda body A, B, C leží na jedné přímce, pokud:
11.Zjistěte, zda body A, B, C leží na jedné přímce, pokud platí:
12.Dané jsou body A, B, C. Zjistěte první souřadnice bodu B tak, aby body A, B, C ležely na jedné přímce. Platí:
13.Napište rovnici přímky, která prochází body A, B pokud platí:
14.Napište rovnice stran trojúhelníku ABC s vrcholy
15.Vypočítejte vektorový součin dvou vektorů:
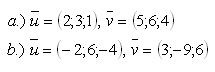
16.Řešte soustavy lineárních rovnic:
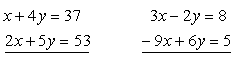
17.Řešte soustavu lineárních rovnic:
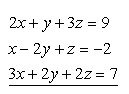
18. Řešte soustavu lineárních rovnic:
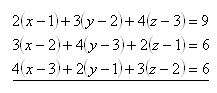
19.K danému determinanty D určitě algebraický doplněk A23
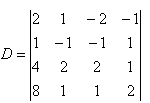
20. Vyčíslete determinant:
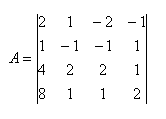
21. Vyčíslete determinant:
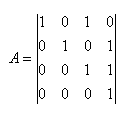
22.Zjistěte, zda body A, B, C, D leží v jedné rovině pokud:
23.Napište obecnou rovnici roviny, která je dána body A, B, C pokud platí:
24.Napište obecnou rovnici roviny, která prochází body A, B, C, pokud
25.Řešte soustavu rovnic:
x + y + z + u = 10
x + y – z – u = 4
x – y + z – u = 2
x – y – z + u = 0