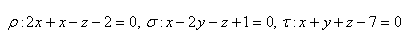Bod, přímka a rovina
1. Vysvětlete v jaké vzájemné poloze může být:
a) bod a rovina
b) přímka a rovina
Řešení:
Bod a rovina.
Bod A [a1; a2; a3] leží v rovině ρ: ax + by + cz + d = 0 jestliže jeho souřadnice splňují rovnici roviny ρ.
Bod A [a1; a2; a3] neleží v rovině ρ: ax+by+cz+d = 0 jestliže jeho souřadnice nesplňují rovnici roviny ρ.
Vzdálenost bodu A [a1; a2; a3] od roviny ρ: ax + by + cz + d = 0 určíme:
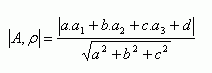
Přímka a rovina.

2.Který z bodů A [3, 2, 7], B [0; 2; 1], C [-8; -2; -1] leží v rovině τ: 2x - 3y - 2z +8 = 0. Jaká musí být hodnota x, aby bod M [x; -6; 2] ležel také v dané rovině?
Řešení:
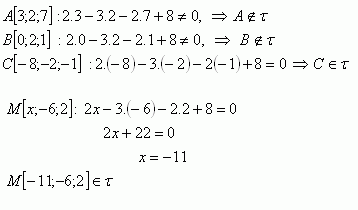
V rovině τ leží body C [-8;-2;-1] a M [-11;-6;2].
3. Zjistěte zda bod A [9; -2; 0] leží v rovině ξ: 3x + 2y - 6Z +26 = 0. Pokud neleží, vypočítejte jeho vzdálenost od dané roviny.
Řešení:
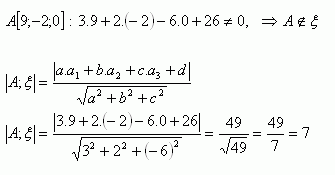
Bod A neleží v rovině ξ . Jeho vzdálenost od této roviny je 7 jednotek.
4.Vypočítejte vzdálenost začátku souřadnicové soustavy od roviny:
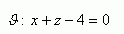
5.Určete vzájemnou polohu rovin ρ a τ. Pokud jsou rovnoběžné různé, určitě i jejich vzdálenost.
Rovnice rovin jsou:

6.Co musí platit pro souřadnici y bodu A [1; y; 0], aby jeho vzdálenost od roviny τ: 3x - 2y - 6Z = 0 byla 5j.
Pro zobrazení řešení se přihlaste.
7. Zjistěte vzájemnou polohu a průsečík přímky a roviny, pokud jsou navzájem různoběžné.
τ: x +y + z +1
Přímka:
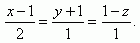
8. Daná je přímka p a rovina ρ. Zjistěte jejich společný bod a odchylku přímky od roviny. Jejich rovnice jsou:
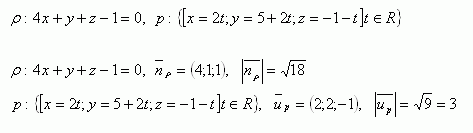
9.Určete vzájemnou polohu rovin ρ a π, jejichž rovnice jsou:
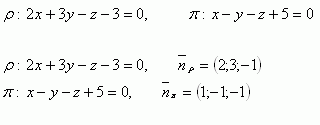
10.Vypočtěte úhel dvou různoběžných rovin:
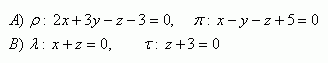
11.Určitě společný bod přímky pa roviny τ jestliže platí:
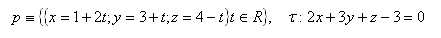
12.Vzdálenost bodu A od roviny σ představuje stranu čtverce ABCD. Vypočítejte obsah tohoto čtverce jestliže platí:
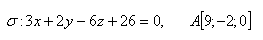
13.Vypočítejte vzdálenost dvou rovnoběžných rovin σ a τ jestliže platí:
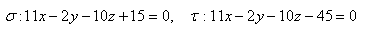
14.Vypočítejte délku výšky sestrojené z vrcholu V v čtyřstěnu ABCV, pokud platí:
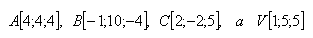
15.Určete reálná čísla a, b, aby roviny π a τ byly rovnoběžné, jestliže platí:
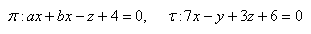
16.Určete vzájemnou polohu rovin σ a η jestliže platí:
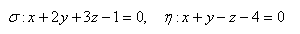
17.Ukažte, že souřadnicové roviny xy a yz jsou navzájem kolmé.
Pro zobrazení řešení se přihlaste.18.Určete úhel přímky p s rovinou μ jestliže platí:
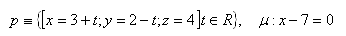
19.Vrcholy čtyřstěnu jsou body A, B, C, D. Určitě odchylku hrany AD od roviny ρ = ABC jestliže platí:
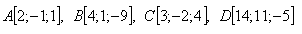
20.Určete vzájemnou polohu tří rovin jestliže platí: