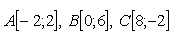Vektor v rovině
1. Charakterizujte vlastnosti vektoru v rovině:

2. Dané jsou body A[-2;5], B[1;yB] a C[4;-3].
a) vektory AB a AC jsou kolmé
b) vektory AB a AC jsou rovnoběžné
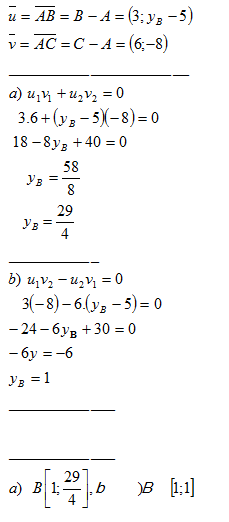
3. Daný je vektor v = AB – A[1;1], B[b1;b2] a stred vektoru S[4;5].
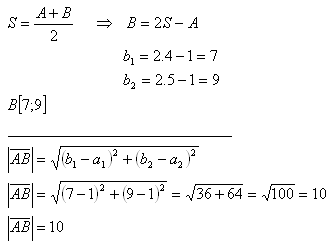
Bod B má súradnice B[7;9]. Veľkosť vektora je 10 jednotiek.
4. Dané jsou body A[2;-3] a B[x;0].
5. Dokažte, že trojúhelník, jehož vrcholy jsou body A [-3; -2], B [1; 4] a C [-5; 0] je rovnoramenný.
Pro zobrazení řešení se přihlaste.6. Dané jsou vektory a = (3;-2) a b = (-1;5).
a.c = 17
b.c = 3
7. Najděte vektor v, kolmý na vektor u = (3, 4) a jehož velikost je 15.
Pro zobrazení řešení se přihlaste.8. Vrcholy Vrcholy trojuholníka ΔABC tvoří body A[1;1], B[2;-1] a C[3;2].
9.Na souřadnicových osách najděte bod, který má od bodu A [4; -6] vzdálenost 5.
Pro zobrazení řešení se přihlaste.10.Vrcholy čtyřúhelníku jsou v bodech: A [0; 0], B [3, -4], C [6; 0] a D [3, 4].
11.Body A, B, C jsou vrcholy trojúhelníku ABC. Ukažte, že trojúhelník ABC je rovnostranný. Vypočítejte jeho obsah.
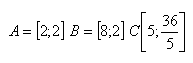
12. Body A, B, C jsou vrcholy trojúhelníku ABC. Středy stran AC, BC označte M, N. Ukažte, že střední příčka MN je rovnoběžná se stranou AB a že platí MN = 0,5 AB.
13. Je dán rovnoramenný lichoběžník ABCD s vrcholy
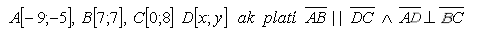
Určete souřadnice bodu D.
14.Určete souřadnice středu S a velikost poloměru r kružnice, která prochází body A, B, C. Řešte pro body:
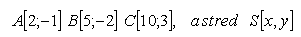
15. Najděte souřadnice těžiště soustavy čtyř stejně hmotných těles, které leží v bodech A, B, C, D. Těžiště T je střed úsečky, jejíž koncové body jsou ve středu vektorů
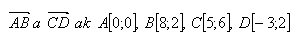
16.Bod A [2; 5] je začátek síly F, jejíž průmět na souřadnicové osy x = 3; y = 3. Vypočítejte konec vektoru, který zobrazuje sílu F.
17. Dané jsou tři body A,B,C
- a.) Dokážte, že leží na jedné přímce
- b.) Zjistěte v jakém poměru jsou velikosti vektorů
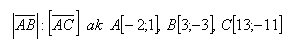
18. Rovnoramenný trojúhelník ABC má základnu AB s vrcholem A a středem základny S. Jeho vrchol C leží na ose x. Určitě vrcholy trojúhelníku B a C.
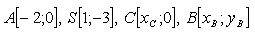
19. Je dán vektor u = (5 ;-3) a takový vektor v = (1;yv) že platí
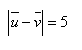
Určete yv
20. Body A, B, C jsou vrcholy trojúhelníku ABC a body M, N, P jsou středy stran tohoto trojúhelníku. Určitě souřadnice tří vektorů, jejichž umístění splývá s těžnice trojúhelníku ABC tak, že počáteční bod je vždy ve vrcholu trojúhelníku. Vypočítejte velikosti těchto vektorů.