Důkazy
1. Jak dokazujeme pravdivost matematické věty?
Řešení:

2.Přímým důkazem dokažte větu:
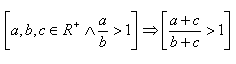
Řešení:
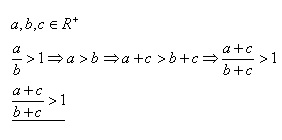
Co platí podle předpokladu.
3.Přímým důkazem dokažte větu:
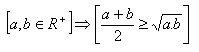
Řešení:
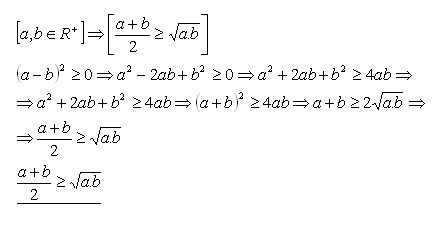
Platí pro všechny a,b z R+
4.Přímým důkazem dokažte větu:
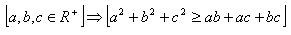
5.Přímým důkazem dokažte větu:
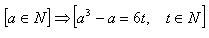
6.Nepřímým důkazem dokažte větu: Pokud a2 je přirozené číslo dělitelná 3, pak i a je přirozené číslo dělitelná 3.
Pro zobrazení řešení se přihlaste.
7.Nepřímým důkazem dokažte větu: Pro přirozené číslo a platí: Pokud a4 + 2 není dělitelné 3, pak a je dělitelné 3.
Pro zobrazení řešení se přihlaste.
8.Dokažte sporem větu: Pro všechny kladné reálná čísla a, b platí:
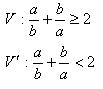
9.Dokažte sporem větu: Číslo √ 3 je iracionální
Pro zobrazení řešení se přihlaste.
10. Matematickou indukcí dokažte větu: Pro všechna přirozená čísla n platí:
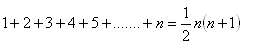
11.Matematickou indukcí dokažte větu: Pro všechna přirozená čísla n platí:
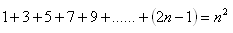
12.Matematickou indukcí dokažte větu: Pro všechna přirozená čísla n platí:
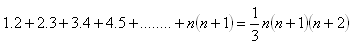
13. Matematickou indukcí dokažte větu: Pro všechna přirozená čísla n platí:
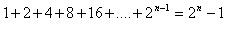
14.Matematickou indukcí dokažte větu:
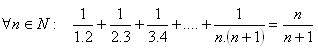
15.Matematickou indukcí dokažte větu:
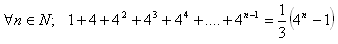
16.Matematickou indukcí dokažte Moivreovu větu:
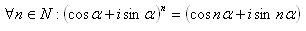
17.Uvnitř trojúhelníku Δ ABC je dán bod U. Dokažte, že platí vztah:
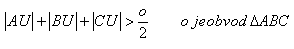
18.Dokažte větu: těžnice trojúhelníku je menší než polovina obvodu.
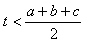
19.Dokažte větu:
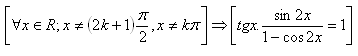
20.Rovnostrannému válci je vepsána koule a kužel. Podstava kužele je shodná s podstavou válce, vrchol kužele je ve středu druhé podstavy. Ukažte, že Archimedova úloha platí. (Archimedes asi 287–212 pred n. l.)