Pravděpodobnost

1. Definujte a charakterizujte pravděpodobnost.

Řešení:

a) Klasická definice pravděpodobnosti:
Nechť náhodný pokus splňuje předpoklady

• Počet všech výsledků je konečný
• Všechny výsledky jsou stejně možné
• Žádné dva výsledky nemohou nastat současně

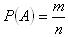Pravděpodobnost jevu A je číslo , kde n je počet všech možných výsledků náhodného pokusu am je počet všech příznivých výsledků, tj. výsledků, při kterých nastane jev A..

Platí : 0 ≤ P(A) ≤ 1
Pravděpodobnost nemožného javu : P(A) = 0
Pravděpodobnost jistého javu: P(A) = 1

b) Podmíněná pravděpodobnost A za podmínky B je číslo:



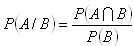
c) Pravděpodobnost nezávislých jevů:

P(A∩B) = P(A)P(B)

d) Pravděpodobnost neslučitelných jevů:

P(AUB) = P(A) + P(B)

e) Binomické rozdělení pravděpodobnosti:

Nechť A je jev s pravděpodobností P. Pak pravděpodobnost, že při n-násobném opakování pokusu, jev A nastane právě k-krát je číslo:



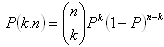
f) Hypergeometrické rozdělení pravděpodobnosti.

Nechť V předmětů vybraných z N předmětů má určitou vlastnost, pak NV předmětů tuto vlastnost nemá.
Pravděpodobnost, že právě k předmětů z řad n náhodně vybraných předmětů tuto vlastnost má, je číslo:

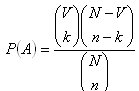
2.Z osmnácti lístků označených čísly 1 - 18 vytáhneme náhodně jeden lístek. Jaká je pravděpodobnost, že na vytažením lístku bude:

Řešení:

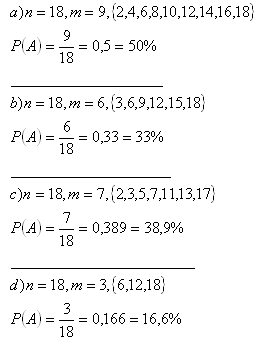
3. Jaká je pravděpodobnost že při hodu dvěma kostkami (červené a modré) padne:

Řešení:

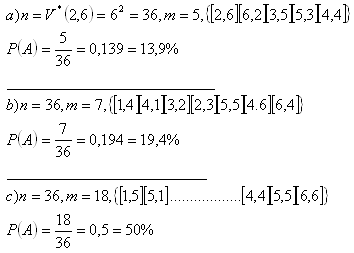
4. Hazardní hráč hází třemi kostkami, položil G. Galileimu otázku: "Mám vsadit na součet 11 nebo součet 12?" Co mu Galilei odpověděl?

5. Dlouhodobé výzkumy na stejném území ukázala, že ze 100 000 dětí se 82 170 dožije 40 let a 37 930 se dožije 70 let. Jaká je pravděpodobnost, že člověk, který se dožije 40 let, dožije se i 70 let?

6. Ve městě jsou čtyři křižovatky se světelnými semafory. Každý z nich uvolňuje nebo uzavírá dopravu se stejnou pravděpodobností 0,5. Jaká je pravděpodobnost, že auto:

7. V 32 hracích kartách jsou 4 esa a 12 figur (4 králové, 4 horníci a 4 spodci). Jaká je pravděpodobnost, že náhodně vytažena jedna karta bude eso nebo figura?

8. Otcové jsou šťastní, když se jim narodí syn. Z dlouhodobých statistik je známo, že pravděpodobnost narození chlapce je P (A) = 0,51.

9.     V šestnácti lahvích jsou minerálky. Víme, že v 10 láhvích je Slatina av 6 lahvích je Baldovská. Jaká je pravděpodobnost, že mezi 4 náhodně vybranými lahvemi jsou 2 Slatiny a 2 Baldovaké?

10. V hazardnej číselnej hre sa losuje 6 čísiel zo 49 čísiel. Aká je pravdepodobnosť získať:

Zaregistruj se a odemkni všechny řešení!

Na priklady.eu najdeš spoustu cvičení, vzorových řešení a užitečných materiálů.
Registrovaní uživatelé vidí celý obsah – bez omezení!
Stačí se přihlásit a začít se učit efektivně.

Zaregistruj se nyní a začni s učením!

Máš už vytvořený účet? Přihlas se