Pravoúhlý trojúhelník

1. Definujte pravoúhlý trojúhelník.

Řešení:


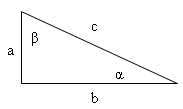
a) Pytagorova věta:

a² + b² = c²

b) Goniometrické funkce:



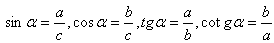
c) Obvod trojúhelníka:

O = a + b + c

d) Obsah trojúhelníka:



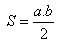
c) Euklidove věty:

a² = c.c_a
b² = c.c_b
v² = c_a.c_b

2. V pravoúhlém trojúhelníku ΔABC jsou dány odvěsny a = 3 cm, b = 4 cm,

Řešení:


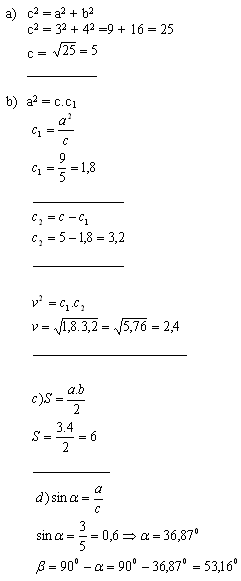
V trojúhelníku ΔABC platí: c = 5cm, v_c = 2,4cm, S = 6cm², α = 36,87°, β = 53,16°.

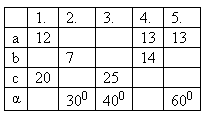
3. V pravoúhlém trojúhelníku jsou a, b odvěsny, c přepona, α je úhel proti odvést a.

Doplňte tabulku! (Délky stran jsou v cm)

Řešení:

4. Strany pravoúhlého trojúhelníku tvoří aritmetickou posloupnost. Vypočtěte:

5.     Určitě obvod pravoúhlého trojúhelníku, jestliže součet jeho odvěsen je 30 cm a jeho obsah je 110,5 cm².

6. Vypočtěte velikost základny a ramene rovnoramenného trojúhelníku, pokud rameno je o 1 cm delší než základna a výška na základnu je o 2 cm kratší než rameno.

7. Dokažte, že trojúhelník má strany a = 4p²-1, b = 4p, c = 4p² +1 je pravoúhlý a jmenuje se pythagorejský trojúhelník. Napište čtyři takové trojúhelníky.

8. Jaké stoupání má cesta, pokud na dopravní značce, která o tom informuje, je napsáno 6,7%? Auto prošlo 2,3 km po této cestě.

9. Vypočítejte obsah rovnoramenného pravoúhlého trojúhelníku, jehož obvod je 20cm.

10. Pro odvěsny pravoúhlého trojúhelníku platí a: b = 2:3. Přepona má délku 10 cm.

Zaregistruj se a odemkni všechny řešení!

Na priklady.eu najdeš spoustu cvičení, vzorových řešení a užitečných materiálů.
Registrovaní uživatelé vidí celý obsah – bez omezení!
Stačí se přihlásit a začít se učit efektivně.

Zaregistruj se nyní a začni s učením!

Máš už vytvořený účet? Přihlas se