Molmasse
1. Berechne die Masse in Gramm eines Wasserstoffmoleküls und eines Wasserstoffatoms.
Lösung:
Die molare Masse von molekularem Wasserstoff (H2) beträgt 2,016 g·mol-1. Durch Einsetzen in die Gleichung zur Berechnung der Masse pro Molekül erhält man:
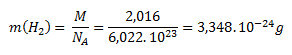
Die molare Masse von atomarem Wasserstoff (H) beträgt 1,008 g·mol-1. Die Masse eines einzelnen Wasserstoffatoms wird analog zum Molekül berechnet:
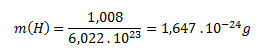
Die Masse eines Wasserstoffmoleküls beträgt 3,348 × 10-24 g und die eines Wasserstoffatoms 1,647 × 10-24 g.
2. Für ein Experiment benötigst du genau 0,1 mol Zink. Welche Masse an Zink muss abgewogen werden?
Lösung:
Wir beginnen mit der Beziehung für die molare Masse. Die molare Masse von Zink aus Tabellen beträgt 65,38 g·mol-1.
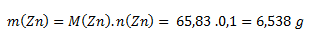
Man muss 6,538 g Zink abwiegen.
3. Kupfer ist ein Gemisch der isotopen Nuklide 63Cu und 65Cu. Die Atommassen dieser Nuklide sind: 63Cu = 62,929 u und 65Cu = 64,928 u (u bezeichnet atomare Masseneinheiten – der Zahlenwert der relativen Atommasse eines Elements und die Masse eines Atoms dieses Elements in u sind gleich). Wenn die relative Atommasse von Kupfer 63,546 beträgt, wie groß ist die prozentuale Häufigkeit der beiden Nuklide im Gemisch?
Lösung:
Die gegebene relative Atommasse von Kupfer ist der gewichtete Mittelwert und hängt von den prozentualen Häufigkeiten der beiden Nuklide im Gemisch ab. Wenn wir die prozentualen Häufigkeiten mit x und y bezeichnen, gelten folgende Gleichungen:
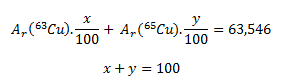
Da die Zahlenwerte der Atommassen in u gleich den relativen Atommassen sind, gilt Ar(63Cu) = 62,929 und Ar(65Cu) = 64,928. Durch Einsetzen dieser Werte erhält man:
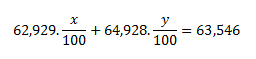
Setze y = 100 − x
0,62929x + 0,64928(100 − x) = 63,546
Die Lösung der Gleichung ergibt die prozentuale Häufigkeit des Nuklids 63Cu:
x = 69,13%
Häufigkeit des Nuklids 65Cu:
y = 100 − x = 100 − 69,13 = 30,87%
Das Gemisch enthält 69,13% 63Cu und 30,87% 65Cu.
4. Berechne die Anzahl der Teilchen des Wirkstoffs in einem homöopathischen Präparat, das durch die Hahnemannsche Centesimalverdünnung C12 hergestellt wird. Dabei wird aus der Urtinktur 1 Teil Lösung entnommen, 99 Teile reines Lösungsmittel hinzugefügt, gemischt und dies insgesamt zwölfmal wiederholt (Verdünnung C12). Die Urtinktur enthält 1 g NaCl in 1 Liter destilliertem Wasser.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5. Bestimme das chemische Äquivalent von Kupfer in einem Oxid, in dem Kupfer mit Sauerstoff im Massenverhältnis 3,971 : 1,000 verbunden ist.
Bitte melden Sie sich an, um die Lösung anzuzeigen.6. Wie groß muss die Masse von Calcium sein, damit die Probe die gleiche Anzahl Atome enthält wie 10,00 g Zink?
Bitte melden Sie sich an, um die Lösung anzuzeigen.7. Natürliches Lithium ist ein Gemisch der Nuklide 6Li und 7Li mit prozentualen Häufigkeiten von 7,54% und 92,46%. Berechne die relative Atommasse des Nuklids 7Li, gegeben dass die relative Atommasse von 6Li 6,016 beträgt und die durchschnittliche relative Atommasse von natürlichem Li 6,941 ist.
Bitte melden Sie sich an, um die Lösung anzuzeigen.8. Die Masse eines Atoms eines bestimmten Elements beträgt 3,158 × 10-22 g. Berechne die relative Atommasse (d.h. molare Masse) des Elements und bestimme, um welches Element es sich handelt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.9. Berechne die Stoffmenge des Kristallwassers in 50,4 g Eisen(II)-sulfat-Heptahydrat.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
10. Berechne die Stoffmenge:
- a) 5,32 × 1021 Atome Quecksilber (wie in Beispiel 2)
- b) 50 g Quecksilber (wie in Beispiel 2)
- c) wasserfreies Calciumsulfat in 100 g Calciumsulfat-Dihydrat (wie in Beispiel 9)