Geometrische Bedeutung der Ableitung

1.Was ist die geometrische Bedeutung der Ableitung?

Lösung:

Mit Hilfe der Ableitung der Funktion y = f(x) können wir die Gleichung der Tangente oder die Gleichung der Normalen an den Graphen der Funktion im Punkt T [xT , yT] aufstellen.

Gleichung der Tangente:

y−yT=kt(x−xT),kt=f′(xT)y - y_T = k_t (x - x_T), \quad k_t = f'(x_T)

Gleichung der Normalen:

y−yT=kn(x−xT),kn=−1f′(xT)y - y_T = k_n (x - x_T), \quad k_n = -\frac{1}{f'(x_T)}

Der Punkt T [x_T, f(x_T)] ist der gemeinsame Punkt der Tangente (oder Normalen) mit dem Graphen der Funktion.

Subtangente und Subnormale:

Die Tangente, die Normale und die x-Achse bilden ein rechtwinkliges Dreieck Δ ABT (Rechter Winkel im Scheitelpunkt T).

Es gilt:

  • Der Punkt T liegt auf der Geraden t,

  • Der Punkt A liegt auf der Geraden t ∩ x-Achse,

  • Der Punkt B liegt auf der Geraden n ∩ x-Achse.

  • Der Punkt T₁ [x_T; 0] ist die orthogonale Projektion des Punktes T auf die x-Achse.

Subtangente Sₜ ist die Länge der Strecke ∣AT1∣|AT_1|:

St=∣yy′∣S_t = \left| \frac{y}{y'} \right|

Subnormale Sₙ ist die Länge der Strecke ∣T1B∣|T_1B|:

Sn=∣y⋅y′∣S_n = |y \cdot y'|

Länge der Tangentenstrecke TA = t:

t2=yr2+St2t^2 = y^{2} + S_t^{2

Länge der Normalenstrecke TB = n:

n2=yr2+Sn2n^2 = y^{2} + S_n^{2}

2. Bestimme die Gleichung der Tangente und die Gleichung der Normalen an die Kurve:

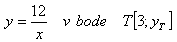
geometricky-vyznam-derivacie-2z

Lösung:

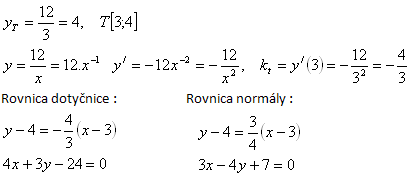
geometricky-vyznam-derivacie-2r

Gleichung der Tangente                     Gleichung der Normalen

3. Bestimme die Gleichung der Tangente und die Gleichung der Normalen an die Kurve:

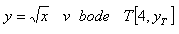
geometricky-vyznam-derivacie-3z

Lösung:

geometricky-vyznam-derivacie-3r

Gleichung der Tangente                      Gleichung der Normalen

4. Bestimme die Gleichung der Tangente und die Gleichung der Normalen an die Kurve:


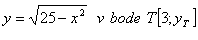
geometricky-vyznam-derivacie-4z
Bitte melden Sie sich an, um die Lösung anzuzeigen.

5. Bestimme die Gleichung der Tangente und die Gleichung der Normalen an die Kurve:

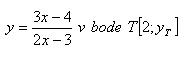
geometricky-vyznam-derivacie-5z
Bitte melden Sie sich an, um die Lösung anzuzeigen.

6. Bestimme die Gleichung der Tangente und die Gleichung der Normalen an die Kurve y = ln(x+1) im Punkt T[0; yT]

Bitte melden Sie sich an, um die Lösung anzuzeigen.

7. Bestimme die Gleichung der Tangente an die Kurve y = sin 2x im Punkt T [3π/4 ; yT].

Bitte melden Sie sich an, um die Lösung anzuzeigen.

8. Bestimme die Gleichung der Tangente an die Kurve y = x2 – 4x + 3, die mit der x-Achse einen Winkel φ = 450 bildet.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

9. Finde die Gleichung der Tangente an die Kurve y = x2 - 2x + 3, wenn die Tangente parallel zur Geraden p : 3x - y + 5 = 0 ist.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

10. Die Funktion ist gegeben durch f : y = x3 - 9x2 + 15x + 3. Bestimme die Berührpunkte der horizontalen Tangenten.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

11. Bestimme den Winkel φ zwischen zwei Tangenten der Kurve, wenn die eine den Berührpunkt T1[3; yT1] und die andere T2[-3; yT2] hat. Die Gleichung der Kurve:

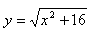
geometricky-vyznam-derivacie-11z
Bitte melden Sie sich an, um die Lösung anzuzeigen.

12. Bestimme die Längen der Subtangente, Subnormalen, Tangente und Normalen zum Graphen der Funktion im Punkt T[1; yT]. Die Funktion hat die Gleichung:

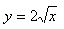
geometricky-vyznam-derivacie-12z
Bitte melden Sie sich an, um die Lösung anzuzeigen.

13. Berechne die Längen der Subtangente, Subnormalen, Tangente und Normalen zum Graphen der Funktion y = 2x im Punkt T [1; yT].

Bitte melden Sie sich an, um die Lösung anzuzeigen.