Kubikvolumen
1.Erklären Sie den Begriff Kubikvolumen – „Kubatur“!
Lösung:
Kubikvolumen – Kubatur ist die Berechnung des Volumens von Rotationskörpern. Wir berechnen das Volumen eines Körpers, der durch das Rotieren einer Ebenenfigur (Rechteck, Dreieck, Trapez, Kreis usw.) um die x-Achse entsteht. Die Ebenenfigur wird begrenzt durch die x-Achse, die Geraden x1 = a, x2 = b und die Kurve y = f(x).
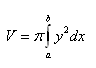
2.Leiten Sie die Formel für das Volumen eines geraden Kreiszylinders mit Grundradius r und Höhe v her.
Lösung:
Der Körper entsteht durch das Rotieren eines Rechtecks um die x-Achse. Das Rechteck wird durch die x-Achse und die Geraden x1=a=0, x2=b=v, y=r begrenzt.
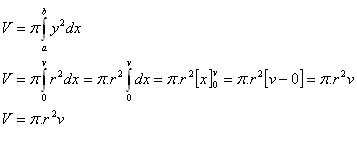
3.Leiten Sie die Formel für das Volumen eines geraden Kreiskegels her, dessen Grundradius r und dessen Höhe v ist.
Lösung:
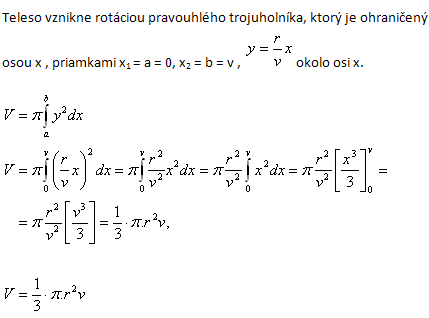
4.Leiten Sie die Formel für das Volumen einer Kugel mit Radius r her!
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5.Leiten Sie die Formel für das Volumen eines Rotationsellipsoids mit den Halbachsen a, b her.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
6.Leiten Sie die Formel für das Volumen eines Rotationsparaboloids her, das durch das Rotieren der Parabel y2 = 2px um die x-Achse entsteht. Das Paraboloid hat die Höhe v.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
7.Berechnen Sie das Volumen des Körpers, der durch das Rotieren der Funktion y = cos x um die x-Achse entsteht.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
8.Leiten Sie die Formel für das Volumen eines Kegelstumpfes her. Die untere Grundfläche hat Radius R, die obere r. Die Höhe des Kegelstumpfes ist v.
Bitte melden Sie sich an, um die Lösung anzuzeigen.