Kugel

1. Beschreibe die Eigenschaften der Kugel und ihrer Teile:

Lösung:

Kugel

r – Radius
d – Durchmesser



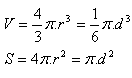
Kugelschale

p1, p2 – Radien der Querschnitte
v – Höhe der Schale



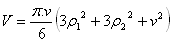
Kugelsegment

r – Radius der Kugel
p – Radius des Segments
v – Höhe des Segments



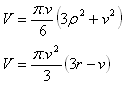
Kugelsektor

r – Radius der Kugel
v – Höhe des Segments



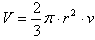
Kugelkalotte oder Kugelzone

r = Radius der Kugel
v = Höhe der Kalotte oder Zone

S = 2π.r.v

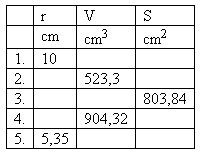
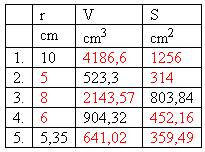
2. Die Tabelle zeigt Werte, die Kugeln charakterisieren.

Vervollständige die Tabelle.

Lösung:

3. Drei Kugeln mit den Radien r₁ = 3 cm, r₂ = 4 cm, r₃ = 5 cm sollen eingeschmolzen und zu einer Kugel gegossen werden.

Lösung:



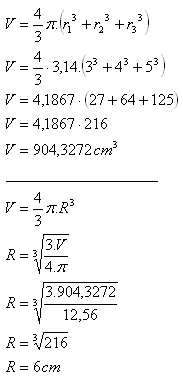
Der Radius der neuen Kugel beträgt R = 6 cm.

4. In eine Kugel mit Radius r = 6 cm ist ein Würfel einbeschrieben.

5. Wie groß ist die Masse einer hohlen Messingkugel (ρ = 8,5 g·cm^-3), wenn der Außendurchmesser D = 12 cm und die Wandstärke h = 2 mm beträgt?

6. Eine Kugel und ein Kegel sind in einen geraden Kreiszylinder einbeschrieben.

7. Ein ebener Schnitt einer Kugel hat eine Länge l = 125,6 cm. Der Abstand der Schnittfläche vom Mittelpunkt der Kugel beträgt v = 6 cm.

8. Ein Kugelsegment mit der Höhe v = 5 cm hat ein Volumen von V = 850 cm³.

9. Die Höhe einer Kugelkalotte entspricht einem Drittel des Kugelradius.

10. Berechne die Masse einer bikonvexen Glaslinse (ρ = 3,5 g·cm^-3) mit einem Durchmesser von 10 cm und einer Dicke von 1,2 cm.

Registrieren Sie sich und schalten Sie alle Lösungen frei!

Auf priklady.eu finden Sie zahlreiche Übungen, Musterlösungen und hilfreiche Materialien.
Registrierte Nutzer haben uneingeschränkten Zugriff auf alle Inhalte!
Einfach einloggen und effektiv lernen.

Jetzt registrieren und loslegen!

Sie haben bereits ein Konto? Dann melden Sie sich an.