Binomialsatz
1.Formuliere den Binomischen Lehrsatz und beschreibe seine Eigenschaften:
Für alle a, b ∈ R, n ∈ N gilt:
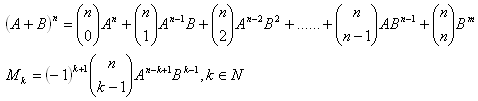
Pascalsches Dreieck
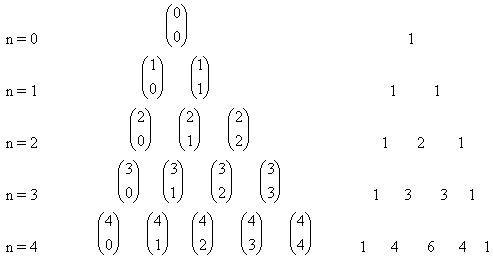
Gilt:
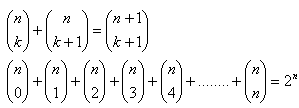
2.Vereinfache:
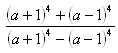
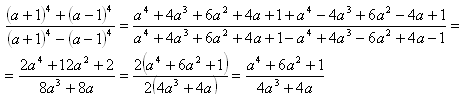
3.Vereinfache:
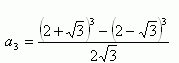
Lösung:
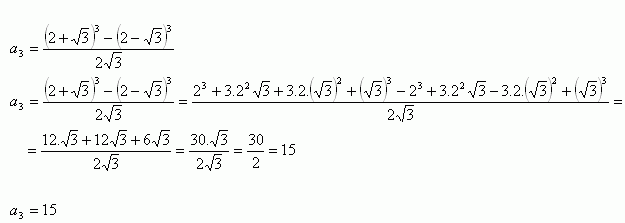
4.Finde das vierte Glied der folgenden Formel nach der Entwicklung:
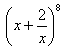
5.Finde das Glied der binomischen Entwicklung von ( x + x-1)8, das kein x enthält.
Bitte melden Sie sich an, um die Lösung anzuzeigen.6.Welches Glied der binomischen Entwicklung von (2x3 + x–1)10 enthält x6?
Bitte melden Sie sich an, um die Lösung anzuzeigen.7.In der Entwicklung von (a + 2a3)n ist der Koeffizient des 3. Gliedes um 44 größer als der Koeffizient des 2. Gliedes.
Finde eine positive ganze Zahl, die diese Bedingung erfüllt.
8.Für welches x ist das 5te Glied der Entwicklung gleich M5 = 105?
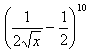
9.Bestimmen Sie, welcher Term der gegebenen Entwicklung x⁷ enthält, wobei gilt:
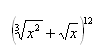
10. Finden Sie den größten Koeffizienten der binomischen Entwicklung (a + b)n, wenn die Summe aller Koeffizienten 4096 beträgt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.