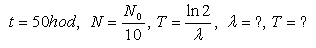Logarithmen – Grundlagen
Logarithmus
Der Logarithmus einer positiven Zahl x zur Basis a (a ist eine positive Zahl, die nicht 1 ist) ist die Potenz y, zu der die Basis a erhoben werden muss, um die Zahl x zu erhalten.
logax = y, weil ay = x a > 0 und a ≠ 1
Eigenschaften der Logarithmen:
a.) Logarithmus eines Produkts: loga(r·s) = logar + logas
b.) Logarithmus eines Quotienten: loga(r/s) = logar − logas
c.) Logarithmus einer Potenz: loga(xn) = n·logax
1. Umschreiben in die Logarithmus-Schreibweise:
102 = 100 log10100 = 2
45 =1024 log41024 = 5
130 = 1 log131 = 0
10-3 = 0,001 log100,001 = -3
640,5 = 8 log648 = 0,5
5-2 = 0,04 log50,04 = -2
2. Löse und begründe:
log101000 log101000 = 3 weil 103 = 1000
log381 log381 = 4 weil 34 = 81
log20,5 log20,5 = -1 weil 2-1 = 0,5
log171 log171 = 0 weil 170 = 1
log1111 log1111 = 1 weil 111 = 11
log50,2 log50,2 = -1 weil 5-1 = 0,2
log150 log150 =
log5(-25) log5(-25) = nicht definiert
log0,40,4 log0,40,4 = 1 weil 0,41 = 0,4
log149 log149 = nicht definiert
3. Bestimme x:
log2x = 3 x = 23 = 8
log10x = -4 x = 10-4 = 0,0001
log16x = 0,5 x = 160,5 = 4
log20x = 1 x = 201 = 20
log25x = -0,5 x = 25-0,5 = 0,2
log0.2487x = 0 x = 0,24870 = 1
4. Bestimme a:
loga25 = 2 a = 5
loga81 = 4 a = 3
loga100000 = 5 a = 10
loga512 = 3 a = 8
loga0,01 = -2 a = 10
loga5 = 0,5 a = 25
loga36 = 2 a = 6
loga64 = 1 a = 64
5. Logarithmiere die folgenden Ausdrücke (zur Basis a):
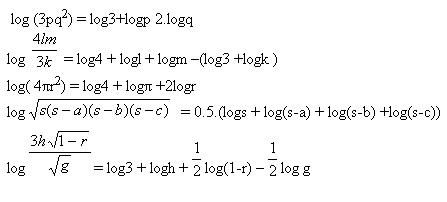
6. Bestimme x:
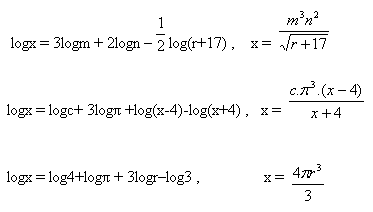
7. Werte den Ausdruck aus:
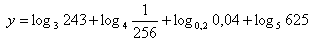
Lösung:
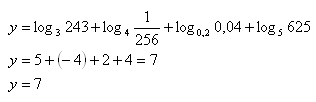
Begründung:
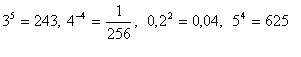
8. Logarithmiere den Ausdruck (zur Basis a):
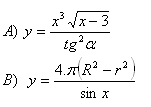
Lösung:

9. Werte den Ausdruck aus:
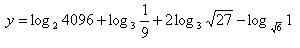
Lösung:
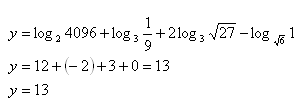
Begründung:
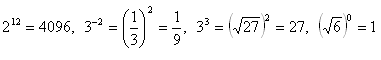
10. Werte den Ausdruck aus:
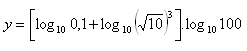
11. Verwende den dekadischen Logarithmus, um die Gleichung zu lösen:
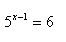
12. Verwende den dekadischen Logarithmus, um die Gleichung zu lösen:
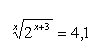
13. Verwende den dekadischen Logarithmus, um die Gleichung zu lösen:
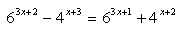
14.Während t = 50 Stunden sinkt die Aktivität von radioaktivem Natrium auf 1/10 des Anfangswerts. Bestimme die Halbwertszeit des Nuklids mit Hilfe des natürlichen Logarithmus.