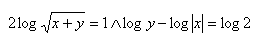Systeme von logarithmischen Gleichungen
1. Löse das Gleichungssystem:
x + y = 34
log2x + log2y = 6 x,y >0 , x < 34
log2x + log2y = 6 x,y >0 , x < 34
Lösung:
x + y = 34
log2x + log2y = 6 x,y >0 , x < 34
y = 34 -x
log2x + log2(34 – x) = 6
log2 ( x.(34 – x)) = log264
x.(34 –x) = 64
x2 – 34x + 64 = 0
(x- 32)( x-2) = 0
x1 = 32 v x2 = 2
y = 34 – x
y1 = 34 – 32 v y2 = 34 - 2
y1 = 2 v y2 = 32
K = {[32,2][2,32]}
x + y = 34
log2x + log2y = 6 x,y >0 , x < 34
y = 34 -x
log2x + log2(34 – x) = 6
log2 ( x.(34 – x)) = log264
x.(34 –x) = 64
x2 – 34x + 64 = 0
(x- 32)( x-2) = 0
x1 = 32 v x2 = 2
y = 34 – x
y1 = 34 – 32 v y2 = 34 - 2
y1 = 2 v y2 = 32
K = {[32,2][2,32]}
2.Löse das Gleichungssystem:
Lösung:
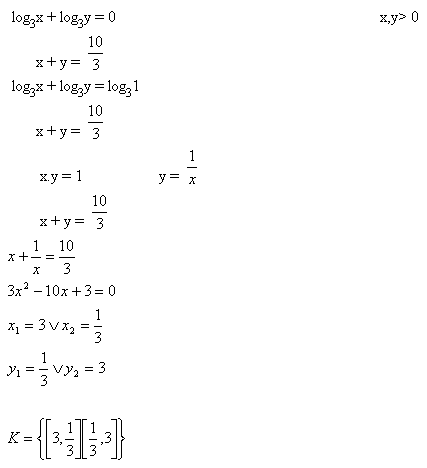
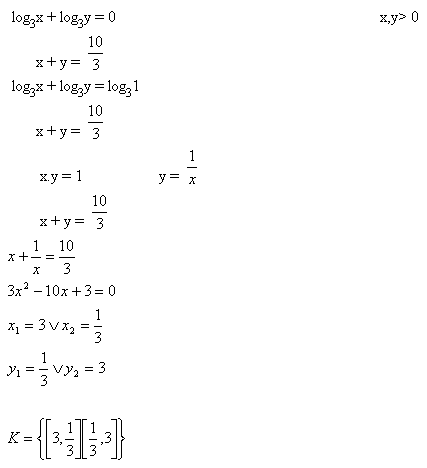
3.Löse das Gleichungssystem:
Lösung:
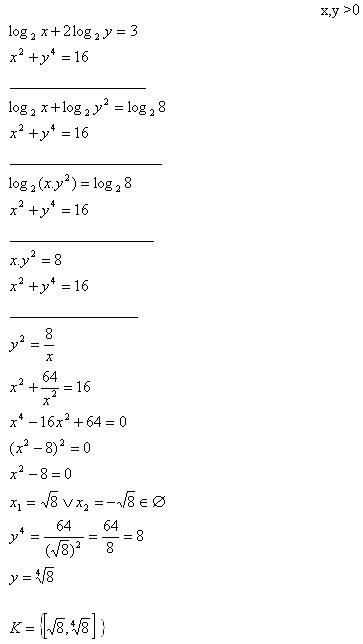
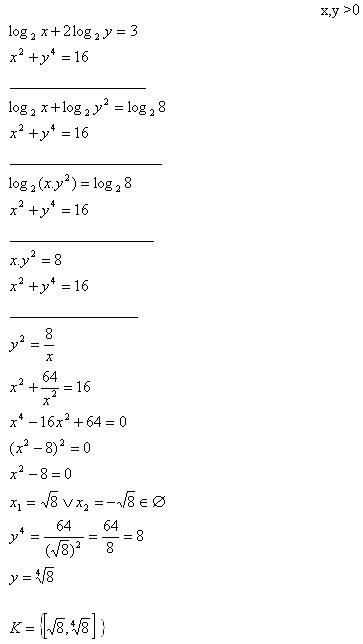
4.Löse das Gleichungssystem:
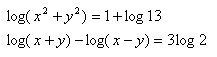x>0, y>0, x>y 5.Löse das Gleichungssystem:
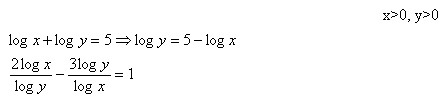
6.Löse das Gleichungssystem:
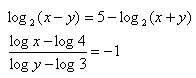x>0, y>0 7.Löse das Gleichungssystem:
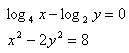x>0, y>0 8.Löse das Gleichungssystem:
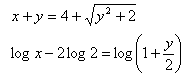x > 0; y > 0 9.Löse das Gleichungssystem:
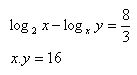
10.Löse das Gleichungssystem:
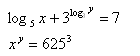x > 0 ; y> 0 Verwende die Formel: 3log3y = y
11.Löse das Gleichungssystem:
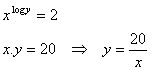
12. Löse das Gleichungssystem:
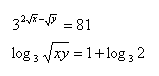
13. Löse das Gleichungssystem:
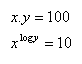
14. Löse das Gleichungssystem:
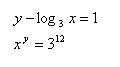
15. Löse das Gleichungssystem:
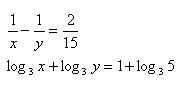
16. Löse das Gleichungssystem:
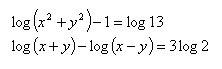
17. Löse das Gleichungssystem:
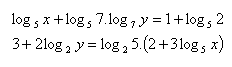
18. Löse das Gleichungssystem:
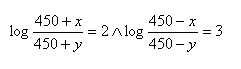
19. Löse das Gleichungssystem:
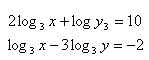
20. Löse das Gleichungssystem:
