Eigenschaften komplexer Zahlen
1.Gegeben seien die komplexen Zahlen a = 1+2i , b = 2 – i. Bestimme a + b, a – b, a·b, a / b, |a|, ferner
Bestimme, ob die Zahl
eine komplexe Einheit ist.
Lösung:
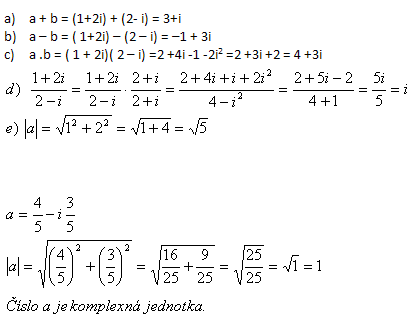
Die Zahl a ist eine komplexe Einheit
2.Schreibe die Zahl
- a) in trigonometrischer Form
- b) in Exponentialform
- c) berechne a5
- d) berechne √a
Lösung:
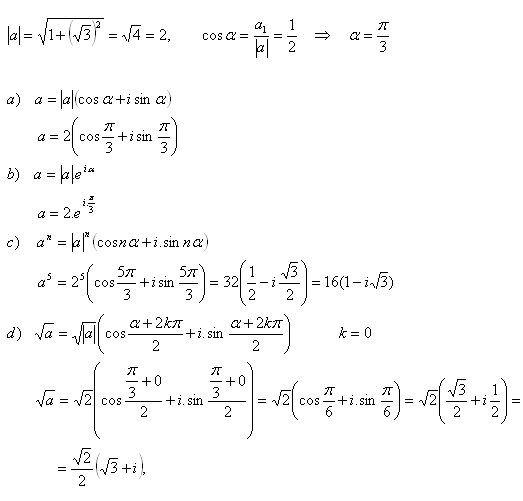
3.Berechne:
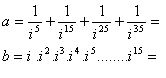
Lösung:
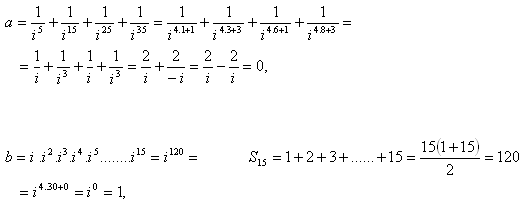
4.Berechne:
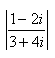
5.Bestimme reelle Zahlen x , y so, dass:
6.Berechne:
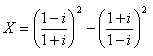
7. Ein Quadrat hat sein Zentrum im Ursprung der gaußschen Zahlenebene, ein Eckpunkt ist das Bild der komplexen Zahl a = 4 + 3i.
- a) Welche komplexen Zahlen stellen die übrigen Eckpunkte dar?
- b) Bestimme den Flächeninhalt dieses Quadrats
Bitte melden Sie sich an, um die Lösung anzuzeigen.
8.Berechne die Länge der Seitenhalbierenden tc des Dreiecks ΔABC, wenn seine Eckpunkte A,B,C die Bilder der komplexen Zahlen a = –1 –i , b = –5 + 7i , c = 9 + 8i sind.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
9.Ein regelmäßiges Sechseck ABCDEF hat das Zentrum S im Ursprung der gaußschen Zahlenebene und den Eckpunkt A im Bild der komplexen Einheit auf der reellen Achse. Bestimme die komplexen Zahlen, deren Bilder an den anderen Eckpunkten des Sechsecks liegen.
Bitte melden Sie sich an, um die Lösung anzuzeigen.