Wahrscheinlichkeit
1.Definiere und charakterisiere Wahrscheinlichkeit.
a) Standarddefinition der Wahrscheinlichkeit
Ein zufälliges Ereignis erfülle die folgenden Bedingungen:
- Die Anzahl der Ereignisse ist endlich
- Alle Ereignisse haben die gleiche Wahrscheinlichkeit, einzutreten
- Keine zwei Ereignisse können gleichzeitig eintreten
Die Wahrscheinlichkeit eines Ereignisses A ist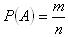 
, n = Anzahl aller möglichen Ereignisse, m = Anzahl der für A günstigen Fälle
Es gilt: 0 ≤ P(A) ≤ 1
Wahrscheinlichkeit eines unmöglichen Ereignisses: P(A) = 0
Wahrscheinlichkeit eines sicheren Ereignisses: P(A) = 1
b) Bedingte Wahrscheinlichkeit eines Ereignisses A unter der Bedingung, dass ein anderes Ereignis B eingetreten ist:
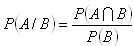
c) Wahrscheinlichkeit zweier unabhängiger Ereignisse:
P(A∩B) = P(A)P(B)
d) Wahrscheinlichkeit zweier sich gegenseitig ausschließender Ereignisse:
P(AUB) = P(A) + P(B)
e) Binomialverteilung der Wahrscheinlichkeit:
Tritt ein Ereignis A mit der Wahrscheinlichkeit P ein, so gilt: Die Wahrscheinlichkeit, dass das Ereignis A in n Versuchen genau k-mal eintritt, ist:
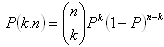
f) Hypergeometrische Wahrscheinlichkeit:
Eine Menge V von N Elementen hat eine Eigenschaft p; folglich haben N-V Elemente die Eigenschaft p nicht.
Die Wahrscheinlichkeit, dass unter n zufällig ausgewählten Elementen k die Eigenschaft p besitzen, ist::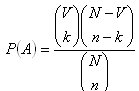 
2.Es gibt 18 Lose mit den Nummern 1 bis 18. Wie groß ist die Wahrscheinlichkeit, ein Los mit der folgenden Eigenschaft zu ziehen:
b) durch 3 teilbare Zahl
c) Primzahl
d) durch 6 teilbare Zahl
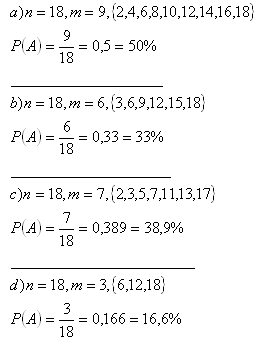
3.Bestimme die Wahrscheinlichkeit folgender Ergebnisse beim Werfen von 2 Spielwürfeln (ein roter und ein blauer):
b) Summe durch 5 teilbar
c) gerade Summe
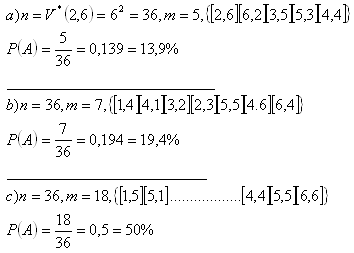
4.Ein Spieler, der mit 3 Würfeln spielt, möchte wissen, ob er auf die Summe 11 oder 12 setzen soll. Welche Summe tritt wahrscheinlicher auf?
Bitte melden Sie sich an, um die Lösung anzuzeigen.5.82 170 von 100 000 Kindern leben 40 Jahre und 37 930 von 100 000 Kindern leben 70 Jahre. Bestimme die Wahrscheinlichkeit, dass eine 40-jährige Person 70 Jahre alt wird.
Bitte melden Sie sich an, um die Lösung anzuzeigen.6.In einer Stadt gibt es 4 Kreuzungen mit Ampeln. Jede Ampel zeigt mit gleicher Wahrscheinlichkeit Grün oder Rot (0,5). Bestimme die Wahrscheinlichkeit für:
b) ein Auto überquert die ersten zwei Kreuzungen ohne anzuhalten
c) ein Auto überquert alle 4 Kreuzungen ohne anzuhalten
7.Ein Kartenspiel mit 32 Karten enthält 4 Asse und 12 Bildkarten. Bestimme die Wahrscheinlichkeit, dass eine zufällig gezogene Karte ein Ass oder eine Bildkarte ist.
Bitte melden Sie sich an, um die Lösung anzuzeigen.8.Bestimme die Wahrscheinlichkeit, dass von 5 geborenen Kindern 3 Jungen sind, wenn die Wahrscheinlichkeit, dass ein Kind ein Junge ist, P(A) = 0,51 beträgt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.9. Auf dem Tisch stehen 16 Colaflaschen. 10 davon sind mit Coca-Cola und 6 mit Pepsi gefüllt. Bestimme die Wahrscheinlichkeit, dass unter 4 zufällig ausgewählten Flaschen 2 Coca-Cola und 2 Pepsi sind.
Bitte melden Sie sich an, um die Lösung anzuzeigen.10.In einem Glücksspiel sind 6 von 49 Zahlen die Gewinnzahlen. Bestimme die Wahrscheinlichkeit für:
b) 4 von 6 Treffer
c) 5 von 6 Treffer
d) 6 von 6 Treffer
