Atomkern

1. Welche Eigenschaften hat der Atomkern?

Lösung:
Der Atomkern bildet den zentralen Teil des Atoms. Er macht fast seine gesamte Masse aus. Der Atomkern enthält Protonen und Neutronen – Nukleonen.

Atomare Konstante:  mu,Ar=1,m=1.6605⋅10−27 kg=931.5 MeV⋅c−2m_u, A_r = 1, m = 1.6605 \cdot 10^{-27} \, \text{kg} = 931.5 \, \text{MeV} \cdot c^{-2}

Proton: p,Ar=1.0072,m=1.673⋅10−27 kg=938.275 MeV⋅c−2
Neutron: n,Ar=1.0086,m=1.673⋅10−27 kg=939.565 MeV⋅c−2

ZAX^A_Z X  Protonenzahl (Anzahl der Protonen im Kern, Elektronen in der Hülle, Ordnungszahl des Elements im Periodensystem)
N=N = Neutronenzahl (Anzahl der Neutronen im Kern)
A=A = Nukleonenzahl A=N+ZA = N + Z (Anzahl der Nukleonen – Protonen und Neutronen im Kern)

Isotope sind Nuklide desselben Elements (gleiches ZZ), die sich in der Neutronenzahl NN unterscheiden (und damit auch in der Zahl AA).

Die Masse des Kerns mjm_j ist immer kleiner als die Masse von ZZ Protonen und NN Neutronen.

Bj=B_j = Massendefekt des Kerns:

mj<Z⋅mp+N⋅mnm_j < Z \cdot m_p + N \cdot m_n mj+Bj=Z⋅mp+N⋅mnm_j + B_j = Z \cdot m_p + N \cdot m_n Bj=(Z⋅mp+N⋅mn)−mjB_j = (Z \cdot m_p + N \cdot m_n) - m_j

mj=Ar⋅mum_j = A_r \cdot m_u

Bindungsenergie des Kerns:

Ej=Bjc2E_j = B_j c^2

Bindungsenergie pro Nukleon:

εj=EjA\varepsilon_j = \frac{E_j}{A}

Neue Masseneinheit:

1 MeV⋅c−2=1.7825⋅10−30 kg1 \, \text{MeV} \cdot c^{-2} = 1.7825 \cdot 10^{-30} \, \text{kg}

1 kg=0.561⋅1030 MeV⋅c−21 \, \text{kg} = 0.561 \cdot 10^{30} \, \text{MeV} \cdot c^{-2} 

2.Blei hat vier Isotope. Bestimmen Sie die Anzahl der Protonen und Neutronen im Kern.

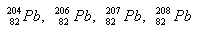
fyzika-atomove-jadro-2z.gif

Lösung:

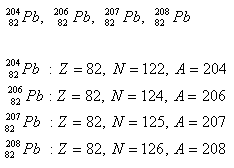
fyzika-atomove-jadro-2r.gif

3. Berechnen Sie:

  • a.) die Ruhemasse des Stickstoffkerns, gegeben Ar(N) = 14,0067
  • b.) die relative Masse des Chlorkerns, gegeben m(Cl) = 5,885·10–26 kg, 1 MeV·c–2 = 1,7825·10–30 kg, mu = 1,6605·10–27 kg

Lösung:

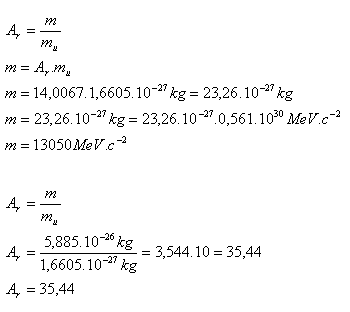
fyzika-atomove-jadro-3.gif 

  • Die Ruhemasse des Stickstoffkerns ist m = 13 050 MeV·c-2.
  • Die relative Masse des Chlorkerns ist Ar = 35.44.

4.Bestimmen Sie den Massendefekt, die Bindungsenergie und die Energie pro Nukleon für einen Radiumkern. Geben Sie die Energie in MeV an.

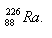
fyzika-atomove-jadro-4z.gif
Bitte melden Sie sich an, um die Lösung anzuzeigen.

5.Bestimmen Sie die prozentuale Zusammensetzung von Chlor mit einer relativen Atommasse von 35,5, das ein Gemisch aus Isotopen ist

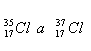
fyzika-atomove-jadro-5z.gif
Bitte melden Sie sich an, um die Lösung anzuzeigen.

6.In der von den Amerikanern über Hiroshima abgeworfenen Atombombe enthielt die Ladung 44,5 kg Uran. Welche Energie wurde freigesetzt?

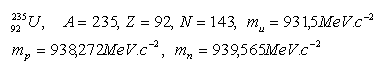
fyzika-atomove-jadro-6z.gif
Bitte melden Sie sich an, um die Lösung anzuzeigen.

7.Wie lange würde ein Kraftwerk, dessen zwei Blöcke eine Leistung von P = 2,440 MW haben, benötigen, um die Energie aus Aufgabe Nr. 6 (E = 3.24·1016 J) zu erzeugen?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

8.Ein Kern mit der Massenzahl 100 und der Bindungsenergie εj1 = 7.4 MeV spaltet sich in zwei Kerne mit der Bindungsenergie pro Nukleon εj2 = 8.2 MeV. Welche Energie wird bei der Reaktion freigesetzt?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

9.Bestimmen Sie die durch die Spaltung von 1 kg Uran gewinnbare Energie 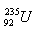fyzika-atomove-jadro-9z.gif wenn die Spaltung eines Urankerns 200 MeV Energie freisetzt. Welche Masse an Steinkohle mit einem Heizwert von 3·107 J·kg würde benötigt, um die gleiche Energie zu erhalten?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

10.Ein Block eines Kernkraftwerks, der Kernenergie mit einem Wirkungsgrad von 40% in elektrische Energie umwandelt, hat eine elektrische Leistung von 600 MW. Bestimmen Sie die Masse an Uran 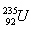fyzika-atomove-jadro-10z.gif die in 24 Stunden verbraucht wird, wenn bei der Spaltung eines einzelnen Kerns 200 MeV Energie freigesetzt werden.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

11.Zeigen Sie, dass für die in der Atomphysik verwendeten Masseneinheiten Folgendes gilt:

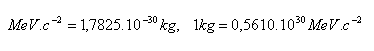
atomove-jadro-11z
Bitte melden Sie sich an, um die Lösung anzuzeigen.

12.Drücken Sie die Masse der Atommassekonstante mu, des Protons mp und des Neutrons mn in Einheiten von MeV c–2 aus.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

13.Bestimmen Sie die Bindungsenergie des Kohlenstoffkerns pro Nukleon.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

14.Bestimmen Sie die Anzahl der Uranatome in 1 kg Uran.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

15.Finden Sie heraus, wie viele Protonen und wie viele Neutronen in 1 kg Neon enthalten sind.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

16.Bestimmen Sie die gesamte Bindungsenergie der Kerne in einem Kilogramm Uran. Ein Kilogramm Uran enthält 2.53×1024 Atome.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

17.Berechnen Sie die Größe der elektrischen Kraft

  • a.)    mit der sich zwei Protonen im Kern abstoßen (r = 10–15 m)
  • b.)    mit der sich ein Proton und ein Elektron anziehen (r = 10–10 m)
Bitte melden Sie sich an, um die Lösung anzuzeigen.

18.Ein Kern mit der Massenzahl A = 230 und der Bindungsenergie pro Nukleon
εj1 = 7.4 MeV spaltet sich in zwei Kerne mit Bindungsenergie pro Nukleon εj2 = 8.3 MeV. Welche Energie wird bei der Spaltung freigesetzt?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

19.Bor, wie es in der Natur vorkommt, ist eine Mischung aus zwei Isotopen. Die mittlere Atommasse von Bor beträgt 10.82 mu. Wie viel Prozent jedes Isotops sind im natürlichen Bor enthalten, wenn:

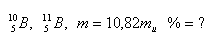
atomove-jadro-19z
Bitte melden Sie sich an, um die Lösung anzuzeigen.

20.Vergleichen Sie die Dichte des Wasserstoffkerns mit der Dichte von Wasser.

Bitte melden Sie sich an, um die Lösung anzuzeigen.