Die Oberfläche der Flüssigkeit
1. Erklären Sie die physikalischen Konzepte der „Oberflächenschicht“ und der „Kapillarität“
Lösung:
Die Oberfläche und ein Flüssigkeitstropfen oder eine Blase verhalten sich, als läge eine elastische Folie auf ihrer Oberfläche – die „Oberflächenschicht“. Sie hat eine Dicke von etwa 10-9 m. Sie wird durch eine Schicht von Molekülen gebildet. Oberfläche und Tropfen haben eine Oberfläche, eine Blase hat zwei Oberflächen.
Oberflächenspannung:
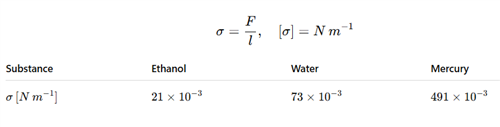
Oberflächenspannungskoeffizienten:
| Stoff | |
|---|---|
| Alkohol | |
| Wasser | |
| Quecksilber |
Für: Oberfläche, Tropfen vs. Blase, Membran
| Größe | Oberfläche, Tropfen | Blase, Membran |
|---|---|---|
| Oberflächenkraft | ||
| Oberflächenenergie | ||
| Kapillardruck | ||
| Hydrostatischer Druck |
l = 2π.r S = π.r2
- Kapillarerhöhung = Anstieg einer benetzenden Flüssigkeit in einer Kapillare
- Kapillarerniedrigung = Absenkung einer nicht benetzenden Flüssigkeit in einer Kapillare
2.Wie groß ist die Masse eines Wassertropfens (σ = 73.10-3 N.m-1), der von einem Rohr mit einem Radius von 0,5 mm abgetropft ist?
Lösung:
Analyse:
R = 0.5·10-3 m, g = 10 m.s-2, σ = 73.10-3 N.m-1
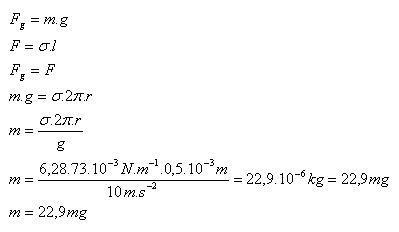
Die Masse des Wassertropfens beträgt m = 22.9 mg.
3.Eine Kapillare maß 100 Tropfen Ethanol mit einer Masse von 1.81 g. Die gleiche Anzahl von Wassertropfen aus derselben Kapillare und bei gleicher Temperatur hat eine Masse von 6.26 g. Bestimmen Sie die Oberflächenspannung von Ethanol σ1, wenn die Oberflächenspannung von Wasser σ2(H2O) = 73.10-3 N.m-1 beträgt.
Lösung:
Analyse:
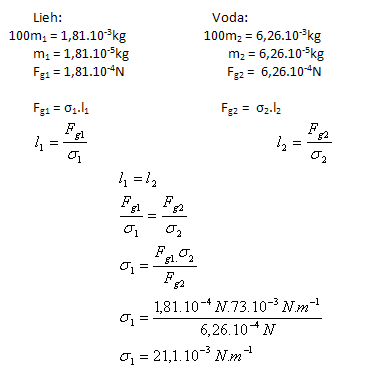
Die Oberflächenspannung von Ethanol ist σ1 = 21.1·10-3 N.m-1
4.Wasser tropft aus einer Kapillare mit dem Radius r = 0.9 mm. Wie viele Wassertropfen sind in 1 cm3 Wasser? (σ = 73.10-3 N.m-1, ρ = 103 kg.m-3)
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5.Eine bewegliche Stange mit einer Länge von 40 mm auf einem Rahmen mit einem Seifenfilm befindet sich im Gleichgewicht, wenn sie mit einem Gewicht von 320 Milligramm belastet wird. Wie groß ist die Oberflächenspannung der Seifenlösung in Wasser im Kontakt mit Luft? Der Film hat zwei Oberflächen. (Die Masse der Stange vernachlässigen)
Bitte melden Sie sich an, um die Lösung anzuzeigen.
6. Bestimmen Sie die Arbeit (in einem isothermen Prozess), die erforderlich ist, um eine Seifenblase mit einem Durchmesser von 14 cm aufzublasen. Die Blase hat zwei Oberflächen. σ = 40·10-3 N.m-1
Bitte melden Sie sich an, um die Lösung anzuzeigen.
7.Eine Seifenblase (σ = 40·10-3 N.m-1) hat einen Radius von 2 cm. Welche Arbeit wird verrichtet, wenn wir ihren Radius um 1 cm vergrößern?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
8. Der Kapillaraufstieg – Erhöhung – von Ethanol in einer engen Kapillare beträgt 12 mm. Wie groß ist der Innendurchmesser der Kapillare? (ρ = 800 kg.m-3, σ = 21.4 mN.m-1)
Bitte melden Sie sich an, um die Lösung anzuzeigen.
9.Die Kapillare hat einen Innendurchmesser von 0.2 mm. Berechnen Sie:
- a.) Wie hoch Benzol in der Kapillare steigt (ρ = 870 kg.m-3, σ = 29,1.10-3N.m-1)
- b.) Wie sich die Steighöhe von Benzol ändert, wenn wir eine Kapillare mit doppeltem Radius verwenden
- c.) Wie sich das Ergebnis des Experiments auf dem Mond ändern würde. (gM = 0.167g)
10. Wie groß ist die Niveaudifferenz in zwei in eine Flüssigkeit (ρ = 800 kg.m-3, σ = 22.10-3N.m-1) eingetauchten Kapillaren? Die Kapillaren haben unterschiedliche Innendurchmesser: d1 = 0.4mm, d2 = 1mm
Bitte melden Sie sich an, um die Lösung anzuzeigen.
11.Auf einem Rahmen mit einer beweglichen Trennwand von 10 cm Länge befindet sich ein Seifenfilm. Welche Arbeit muss verrichtet werden, um die Trennwand um 2 cm zu verschieben?
Bitte melden Sie sich an, um die Lösung anzuzeigen.12.Ein kleiner Rahmen mit einem beweglichen Bügel der Masse 1.2 g befindet sich in vertikaler Lage. Die Gewichtskraft hält den Bügel und den Film im Gleichgewicht. Wie lang ist der Bügel, wenn die Oberflächenspannung des Films 60.10-3N.m-1 beträgt? Wie ändert sich die Oberflächenenergie des Films, wenn der Bügel um 2 cm verschoben wird?
Bitte melden Sie sich an, um die Lösung anzuzeigen.13.Ein Wassertropfen mit einem Radius von 3 mm wird in winzige Tröpfchen mit einem Radius von 3.10-5 mm zerstäubt. Um wie viel vervielfacht sich dabei die Oberflächenenergie der Wassertropfen?
Bitte melden Sie sich an, um die Lösung anzuzeigen.14.Wie groß ist der Luftdruck in einer Seifenblase mit einem Radius von 2 mm, wenn der atmosphärische Druck 101325 Pa beträgt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.15.In einer Kapillare stieg Kerosin auf eine Höhe von 13 mm, und in einer anderen Kapillare mit demselben Radius sank Quecksilber um 13.9 mm. Wie groß ist die Oberflächenspannung von Quecksilber, wenn die Dichte von Quecksilber 13.6.103 kg.m3 ist? Die Oberflächenspannung von Kerosin beträgt 27.10-3N.m-1 und seine Dichte 0.8.103 kg.m-3.
Bitte melden Sie sich an, um die Lösung anzuzeigen.16. In einer Kapillare mit einem Durchmesser von 2 mm befindet sich Wasser. Wie hoch bleibt eine Wassersäule in der Kapillare stehen, wenn beide Enden offen bleiben?
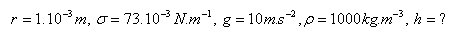
17.Aus einer Kapillare tropften 100 Wassertropfen mit einer Gesamtmasse von 2.4 g. Die Masse von 50 Tropfen Glycerin aus derselben Kapillare beträgt 1.1 g. Wie ist das Verhältnis der Oberflächenspannungen der beiden Flüssigkeiten?
Bitte melden Sie sich an, um die Lösung anzuzeigen.18. Wie groß ist die Oberflächenspannung von Glycerin? (Verwenden Sie das Ergebnis von Aufgabe 17)
Bitte melden Sie sich an, um die Lösung anzuzeigen.19.Wenn N Wassertropfen mit einem Radius von 2.10–6 m zu einem Tropfen mit einem Radius von 2.10–3 m verschmelzen, werden 3.668 mJ Energie frei. Um wie viel erwärmt sich das Wasser?
Bitte melden Sie sich an, um die Lösung anzuzeigen.20.Berechnen Sie die Oberflächenenergie eines Quecksilbertropfens mit einem Volumen von 1 cm3.
Bitte melden Sie sich an, um die Lösung anzuzeigen.