Idealgas
1. Explain the properties of an ideal gas
Solution:
Ein ideales Gas ist kein reales Gas, sondern ein Modell. Seine Moleküle haben vernachlässigbare Größe und identische Massen m0. Stöße zwischen den Molekülen und ihre Aufpralle an den Behälterwänden sind vollkommen elastisch. Die Aufpralle der Moleküle an den Behälterwänden verursachen den Gasdruck. Die Moleküle üben keine Kräfte aufeinander aus. Unter Standardbedingungen (p0 = 101325 Pa, T0 = 273,15 K) nähern sich die Eigenschaften realer Gase denen eines idealen Gases an. Unter diesen Bedingungen hat 1 mol eines beliebigen Gases stets das Volumen V0 = 22,415 × 10-3 m3·mol-1.
Masse eines Gasmoleküls:
m0 = Mm / NA, NA = 6.022 · 1023 mol−1
Quadratische Mittelgeschwindigkeit (rms) eines Moleküls:
vz = √(3kT / m0) = √(3kNAT / Mm) = √(3RmT / Mm)
k = 1.38 · 10−23 J · K−1 (Boltzmann-Konstante)
Rm = k · NA = 8.314 J · K−1 · mol−1 (molare Gaskonstante)
Mittlere kinetische Energie eines einzelnen Moleküls:
E0 = ½ m0 vz2 = 3/2 kT
Druck eines idealen Gases:
p = (2/3) Nv E0
Nv = N / V (Moleküldichte)
p = (1/3) ρ vz2, ρ = (N m0) / V (Gasdichte)
2.Berechnen Sie die quadratische Mittelgeschwindigkeit eines Sauerstoffmoleküls O2 bei einer Temperatur von 0°C!
Lösung:
Analyse:
T = t + 273,15
T = 0 + 273,15 = 273,15
m0 = Ar·mu = 2·16,00·1,66·10-27 = 53,12×10-27 kg
k = 1,38×10-23 J·K-1
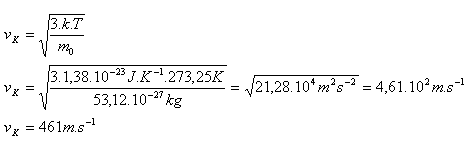
Die quadratische Mittelgeschwindigkeit eines O2-Moleküls ist vK = 461 m·s-1
3.Bestimmen Sie das Verhältnis der quadratischen Mittelgeschwindigkeiten von Wasserstoff- (H2) und Sauerstoff- (O2) Molekülen bei derselben Temperatur.
Lösung:
Analyse:
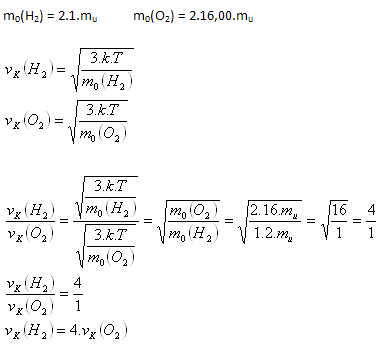
Wasserstoffmoleküle bewegen sich viermal schneller als Sauerstoffmoleküle.
4.Wie groß ist der Luftdruck bei der Temperatur T = 273,15 K, wenn die Masse eines Luftmoleküls m0 = 47,45×10-27 kg und die Luftdichte bei dieser Temperatur ρ = 1,27584 kg·m-3 beträgt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5.Ein ideales Gas mit der Masse m = 3,8×10-2 kg ist in einem Behälter mit dem Volumen von 10 Litern eingeschlossen und hat einen Druck p = 0,49 MPa. Bestimmen Sie die quadratische Mittelgeschwindigkeit der Gasmoleküle.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
6.Berechnen Sie, bei welcher Temperatur die quadratische mittlere Geschwindigkeit von Helium 1300 m·s-1 beträgt, vk = 1300 m·s-1, Ar(He) = 4.003, NA = 6.022·1023 mol-1, k = 1.38·10-23 J·K-1
Bitte melden Sie sich an, um die Lösung anzuzeigen.
7.Wie ändert sich die mittlere kinetische Energie, die ein Molekül eines idealen Gases aufgrund seiner zufälligen Bewegung besitzt, wenn die thermodynamische Temperatur um das Dreifache erhöht wird?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
8.Bestimmen Sie die Änderung der inneren Energie eines idealen Gases mit einatomigen Molekülen, wenn sich seine Temperatur von 200 K auf 400 K erhöht. Das Gas enthält 1028 Moleküle.
Bitte melden Sie sich an, um die Lösung anzuzeigen.9.Wie ändert sich der Druck eines idealen Gases, wenn die Teilchendichte NV dieses Gases um das Vierfache zunimmt und die quadratische mittlere Geschwindigkeit vK unverändert bleibt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
10.Wie groß ist der Druck von Sauerstoff O2 mit einer Dichte von 1,41 kg·m-3 bei einer Temperatur von 00C, wenn seine quadratische mittlere Geschwindigkeit vK = 461 m·s-1 beträgt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
11.Ein ideales Gas mit einer Masse von 6 kg ist in einem Behälter mit einem Volumen von 5 m3 eingeschlossen und steht unter einem Druck von 2·105 Pa. Bestimmen Sie die quadratische mittlere Geschwindigkeit der Gasmoleküle.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
12.Ein Argonatom mit der Geschwindigkeit 500 m·s-1 wird elastisch von der Wand eines Gefäßes reflektiert. Der Geschwindigkeitsvektor des Argonatoms bildet mit der Normale zur Wand einen Winkel a.) 00, b.) 600. Bestimmen Sie in beiden Fällen den Betrag der Impulsänderung nach der vollkommen elastischen Reflexion.
Bitte melden Sie sich an, um die Lösung anzuzeigen.13.Die quadratische mittlere Geschwindigkeit von Chlormolekülen Cl2 beträgt bei 00C 310 m·s-1. Berechnen Sie die Dichte von Chlor bei einem Druck von 105 Pa.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
14.Wie groß ist die mittlere kinetische Energie eines Moleküls eines idealen Gases bei einer Temperatur von -1000C?
Bitte melden Sie sich an, um die Lösung anzuzeigen.