Isoprozesse
1. Was sind Isoprozesse?
Lösung:
Isoprozesse sind Vorgänge in einem idealen Gas mit konstanter Masse, bei denen eine der Zustandsgrößen konstant bleibt.
A) Isothermer Prozess (T = konstant)
Boyle-Mariotte-Gesetz
Die bei einem isothermen Prozess von einem idealen Gas aufgenommene Wärme wird zur Verrichtung von Arbeit verwendet.
B) Isochorer Prozess (V = konstant)
Gesetz von Charles
Die bei einem isochoren Prozess von einem idealen Gas aufgenommene Wärme wird zur Erhöhung seiner inneren Energie genutzt.
C) Isobarer Prozess (p = konstant)
Gay-Lussac-Gesetz
Die bei einem isobaren Prozess von einem idealen Gas aufgenommene Wärme wird sowohl zur Änderung der inneren Energie als auch zur Verrichtung von Arbeit verwendet.
D) Adiabatischer Prozess (Q = 0) – es findet kein Wärmeaustausch zwischen dem Gas und der Umgebung statt. können sich ändern.
Poisson-Gesetz
-
– spezifische Wärmekapazität bei konstantem Druck
-
– spezifische Wärmekapazität bei konstantem Volumen
2.Welches Volumen werden 30 Liter Luft haben, wenn wir bei gleicher Temperatur den Druck von 72 kPa auf 75 kPa erhöhen?
Lösung:
Analyse:
V1 = 30 l = 30·10-3 m3, p1 = 72·103 Pa, p2 = 75·103 Pa, V2 = ?
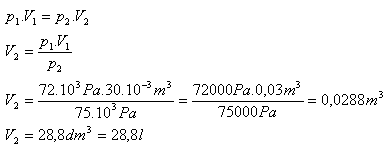
Nach der Druckerhöhung wird die Luft ein Volumen von 28,8 Liter haben.
3.Die Dichte von Helium beträgt bei einem Druck von 105 Pa ρ1 = 0,164 kg·m-3. Wie groß ist seine Dichte, wenn wir es auf einen Druck von 5·107 Pa komprimieren? (Masse und Temperatur des Gases ändern sich während der Kompression nicht).
Lösung:
Analyse:
p1 = 105 Pa, ρ1 = 0,164 kg·m-3 , p2 = 5·107 Pa, ρ2 = ?
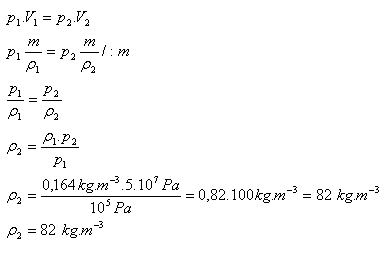
Die Dichte von Helium beträgt nach der Kompression 82 kg·m-3.
4.Die Dichte der Luft unter Normalbedingungen beträgt ρ1 = 1,3 kg·m-3. Wie groß ist die Dichte der Luft, wenn wir sie von Normalbedingungen auf 30oC erwärmen? (Die Menge der Luft ändert sich nicht).
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5.Ein in einem Behälter mit beweglichem Kolben eingeschlossenes Gas wird bei konstantem Druck von 22oC auf 52oC erwärmt. Um wie viel Prozent hat sich sein Volumen vergrößert?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
6. Eine Glühlampe wird bei der Herstellung mit Stickstoff bei einem Druck von 50,6 kPa und einer Temperatur von 18oC gefüllt. Welche Temperatur hat der Stickstoff in der leuchtenden Lampe, wenn sein Druck auf 118 kPa ansteigt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
7.Bei einem Formel-1-Rennen stieg die Temperatur der Luft in den Reifen von 19oC auf 79oC. Wie ändert sich der Druck im Reifen, wenn er ursprünglich auf 240 kPa aufgepumpt war? Warum wird vor dem Start eine „Formationsrunde“ gefahren? (Das Innenvolumen des Reifens ändert sich nicht.)
Bitte melden Sie sich an, um die Lösung anzuzeigen.
8.In einer zylindrischen Kammer befindet sich Luft, die von einem beweglichen Kolben in 50 cm Abstand vom Boden des Zylinders eingeschlossen ist. Der Luftdruck beträgt 105 Pa. Wird der Kolben bei adiabatischer Kompression um 20 cm in Richtung Boden bewegt, steigt der Luftdruck auf 2,05·105 Pa. Bestimmen Sie die Poisson-Konstante für Luft!
Bitte melden Sie sich an, um die Lösung anzuzeigen.
9.Zeigen Sie, dass für einen adiabatischen Prozess T1·V1κ-1 = T2·V2κ-1 gilt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
10. Bei adiabatischer Kompression wurde das Volumen der Luft auf 1/10 des ursprünglichen Volumens verringert. Berechnen Sie Druck und Temperatur der Luft nach der adiabatischen Kompression. Der Anfangsdruck der Luft betrug 105 Pa, die Anfangstemperatur 20oC. κ (Luft) = 1,4
Bitte melden Sie sich an, um die Lösung anzuzeigen.11.Der Druck eines Gases in einem geschlossenen Behälter beträgt bei einer Temperatur von 110C 189 kPa. Wie hoch wird die Temperatur dieses Gases sein, wenn sein Druck auf 1 MPa ansteigt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
12.Der Druck eines Gases beträgt bei einer Temperatur von 200C 107 kPa. Wie hoch wird sein Druck sein, wenn seine Temperatur auf 1500C steigt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
13.Die Temperatur von Sauerstoff gegebener Masse steigt isobar von einer Anfangstemperatur von -200C. Bei welcher Temperatur hat der Sauerstoff das 1,5-fache des Anfangsvolumens?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
14.Welcher Prozess ist in der Tabelle dargestellt:
15.Das Volumen eines Gases beträgt 25 Liter bei einem Druck von 1 kPa. Wie hoch wird sein Druck sein, wenn wir sein Volumen auf 20 % des ursprünglichen Volumens verringern?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
16.Ein zylindrischer Behälter, 30 cm lang, ist mit einem beweglichen Kolben verschlossen. Ein Gas im Behälter steht unter einem Druck von 0,5 MPa. Bestimmen Sie seinen Druck, wenn sich das Innenvolumen des Behälters durch Verschieben des Kolbens um 10 cm vergrößert.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
17.Die mittlere freie Weglänge eines Moleküls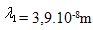 
beträgt bei einem Druck p1 = 105 Pa. Wie groß ist die mittlere freie Weglänge des Moleküls bei einem Druck von
- a.) 1,0 Pa,
- b.) 107 Pa.
18.Wasserstoff H2 hat eine Temperatur von -30C. Durch adiabatische Expansion vergrößert sich sein Volumen auf das Dreifache des ursprünglichen Volumens. Wie hoch ist die resultierende Temperatur des Wasserstoffs während dieses adiabatischen Prozesses?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
19.Argon hat bei Normaldruck p1 = 101325 Pa ein Volumen V1 = 10 Liter. Nach adiabatischer Kompression ändert sich sein Volumen auf V2 = 4 Liter und der Druck auf p2 = 0,468 MPa. Bestimmen Sie die Poisson-Konstante für Argon.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
20.Bestimmen Sie die spezifische Wärmekapazität von Argon bei konstantem Volumen cV, wenn die spezifische Wärmekapazität von Argon bei konstantem Druck
