Lichtinterferenz
1.Erklären Sie das Wesen und die Methoden der Lichtinterferenz.
Lösung:
Interferenz entsteht durch die Überlagerung zweier Lichtwellen, die kohärent sein müssen. Sie müssen die gleiche Frequenz und einen konstanten Phasenunterschied haben. Die Kohärenzbedingung kann von Lichtwellen aus zwei verschiedenen
Quellen nicht erfüllt werden. Sie kann erreicht werden, indem die Lichtwelle einer Quelle in zwei kohärente Wellen aufgeteilt wird. Dies kann erreicht werden:
- a) durch Reflexion der Welle an einem Hindernis – Interferenz durch Reflexion
- b) durch Beugung der Welle an einem Hindernis oder einem Spalt – Interferenz durch Beugung
Interferenzmaximum – Stelle, an der das Licht durch Interferenz verstärkt wird
Interferenzminimum – Stelle, an der das Licht durch Interferenz geschwächt oder ausgelöscht wird.
| Interferenz | Maximum | Minimum |
|---|---|---|
| Durch Reflexion | ||
| Durch Beugung |
k = 1,2,3,....
2.Bestimmen Sie die Dicke der Wand einer Seifenblase (n = 1.33), wenn weißes Licht darauf fällt. Das Interferenzmaximum erster Ordnung wird im grünen Licht beobachtet (fG = 5.7·1014Hz).
Lösung:
Analyse:
n = 1.33, fG = 5.7·1014Hz, c = 3·108m·s-1, d = ? k = 1
Dabei wird die Beziehung für das Interferenzmaximum erster Ordnung bei Reflexion verwendet.
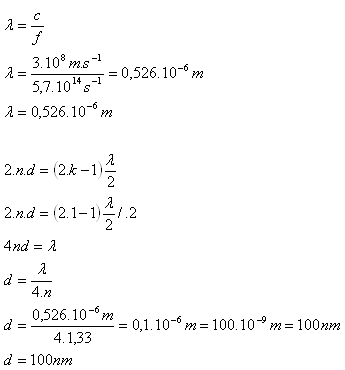
Die Dicke der Seifenblasenwand beträgt d = 100 nm.
3.Die Dicke eines Ölfilms beträgt d = 2.4·10-7m und der Brechungsindex des Öls ist n = 1.5. Welche Farben des reflektierten Lichts werden durch Interferenz ausgelöscht?
Lösung:
Analyse:
Dies ist ein Interferenzminimum bei Reflexion.
d = 2.4·10⁻⁷ m, n = 1.5, λ = ?
k = 1 ⇒ – rotes Licht
k = 2 ⇒ – violettes Licht
k = 3 ⇒ – Ultraviolettstrahlung
Durch Interferenz bei Reflexion werden rotes und violettes Licht sowie unsichtbare Ultraviolettstrahlung ausgelöscht.
4.Eine Glasplatte mit dem Brechungsindex n = 1.5 und der Dicke d = 0.25μm wird mit Licht beleuchtet. Welche Wellenlänge wird im reflektierten Licht maximal verstärkt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5.Wie viele Interferenzmaxima entstehen bei der Beugung von Licht an einem Gitter mit 5000 Linien pro 1 cm, wenn oranges Licht mit λ = 600nm darauf fällt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
6.Ein Beugungsgitter mit 100 Linien pro 1 mm wird senkrecht mit rotem Licht (λ = 700nm) beleuchtet. Bestimmen Sie den Abstand „h“ zwischen dem ersten und dritten hellen Streifen auf einem Schirm, der in der Entfernung l = 1.5m von der Lichtquelle steht.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
7.Wie viele Linien pro 1 mm besitzt ein optisches Gitter, wenn Licht mit der Wellenlänge λ = 589nm im zweiten Maximum um den Winkel α = 43015‘ von der Richtung senkrecht zur Gitterebene abgelenkt wird?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
8.Wie groß muss die maximale Dicke einer Luftschicht sein, in der man bei Licht mit der Wellenlänge 500 nm ein Interferenzmuster beobachten kann, das durch die Reflexion von Strahlen an der Grenzfläche dieser Schicht entsteht?
Bitte melden Sie sich an, um die Lösung anzuzeigen.9.Zwei kohärente Lichtwellen mit der Wellenlänge 600 nm treffen sich an einem Punkt. Bestimmen Sie, ob dort ein Interferenzmaximum oder -minimum auftritt, wenn ihre Phasendifferenz beträgt:
- a.) 300 nm
- b.) 600 nm
- c.) 900 nm
10. Weißes Licht fällt senkrecht auf eine Ölschicht der Dicke d = 0,2 μm auf Wasser. Die Lichtgeschwindigkeit im Öl beträgt
v = 2·108 m·s–1. Welche Farbe wird im Intervall λ : 3,8·10–7 m – 7,8·10–7 m am stärksten verstärkt und welche ausgelöscht?
11.Bestimmen Sie die Dicke eines Seifenfilms (n = 1,33) an den Stellen, an denen der Film im reflektierten Licht blau erscheint. Die Wellenlänge des blauen Lichts beträgt λ = 450 nm = 450·10–9 m = 4,5·10–7 m.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
12.Monochromatisches Licht fällt senkrecht auf ein Beugungsgitter. Auf einem Schirm im Abstand l = 1 m erscheint ein Maximum erster Ordnung im Abstand h = 2 cm vom Maximum nullter Ordnung. Wie groß ist die Wellenlänge des Lichts, wenn
d = 20 μm?
13.Ein schmaler Strahl weißen Lichts fällt auf ein Beugungsgitter mit N1 = 1000 Linien pro 1 mm. Wie würde sich das Bild auf dem Schirm ändern, wenn wir das Gitter durch ein anderes mit N2 = 1500 Linien pro 1 mm ersetzen?
Bitte melden Sie sich an, um die Lösung anzuzeigen.14.Ein Schirm mit sehr kleinen Öffnungen, deren Mittelpunkte 1 mm voneinander entfernt sind, wird senkrecht vor eine Quelle monochromatischen Lichts mit λ = 500 nm gestellt. Wie groß ist der Abstand der dunklen Interferenzstreifen auf dem Schirm? Der Abstand von den Öffnungen zum Schirm beträgt 2,5 m.
Bitte melden Sie sich an, um die Lösung anzuzeigen.15.Monochromatisches Licht mit der Wellenlänge λ = 5·10–7 m fällt auf ein Beugungsgitter mit 500 Linien pro mm. Bestimmen Sie die höchste Ordnung des Spektrums, die bei senkrechtem Einfall auf das Gitter beobachtet werden kann.
Bitte melden Sie sich an, um die Lösung anzuzeigen.16.Wie groß ist die Gitterkonstante eines Gitters, das bei Beleuchtung mit Licht der Wellenlänge λ = 590 nm ein Maximum erster Ordnung im Abstand h = 66 cm auf einem 2 m entfernten Schirm erzeugt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.17.Ein Beugungsgitter mit 100 Linien pro 1 mm wird senkrecht von einem parallelen Strahl roten Lichts (λ = 700 nm) beleuchtet. Bestimmen Sie den Abstand zwischen dem 1. und 3. hellen Streifen auf einem 100 cm entfernten Schirm.
Bitte melden Sie sich an, um die Lösung anzuzeigen.18.Ein Beugungsspektrum wurde mit einem Beugungsspektroskop aufgenommen. Ein Maximum zweiter Ordnung erschien bei einem Winkel α = 30°. Das Gitter wurde mit monochromatischem Licht der Wellenlänge λ = 5,76·10–7 m beleuchtet. Bestimmen Sie die Gitterkonstante. Wie viele Linien hat das Gitter pro 1 mm?
Bitte melden Sie sich an, um die Lösung anzuzeigen.