Reflexion und Brechung

1.Was geschieht, wenn Licht die Grenzfläche zweier Medien durchläuft?

Lösung:

Wenn Licht die Grenzfläche zweier Medien vom ersten Medium (in dem es sich mit der Geschwindigkeit v1 bewegt) in das zweite Medium (in dem es sich mit der Geschwindigkeit v2 bewegt) durchläuft, können zwei Fälle auftreten:

  • Reflexion des Lichts
  • Brechung des Lichts

Lichtreflexion:

Reflexion des Lichts tritt auf, wenn Licht auf ein Medium trifft, in das es nicht eindringen kann.

Reflexionsgesetz:
α=α′\alpha = \al 
Der Reflexionswinkel α′\alpist gleich dem Einfallswinkel α. Der reflektierte Strahl liegt in der Einfallsebene.

Totale Reflexion – Brechung des Lichts von einem optisch dichteren Medium in ein optisch weniger dichtes Medium. (β=90∘\beta = 90^\circ)

sin⁡αm=1n1,n2=1,αm=Grenzwinkel\sin \alpha_m = \frac{1}{n_1}, \quad n_2 = 1, \quad \alpha_m = \text{critical angle}

Lichtbrechung:

Brechung des Lichts tritt auf, wenn Licht in ein anderes Medium eintritt.

Brechungsgesetz (Snelliussches Gesetz):

sin⁡αsin⁡β=v1v2=n2n1\frac{\sin \alpha}{\sin \beta} = \frac{v_1}{v_2} = \frac{n_2}{n_1}

  • α\alpha = Einfallswinkel,

  • β\beta = Brechungswinkel,

  • n1n_1 = Brechungsindex des ersten Mediums,

  • n2n_2 = Brechungsindex des zweiten Mediums.

Wenn β<α\beta < \alpha, wird der Strahl zum Lot hin gebrochen.
Wenn β>α, wird der Strahl vom Lot weg gebrochen.

Absoluter Brechungsindex:

n=cv=cλf=λ0λn = \frac{c}{v} = \frac{c}{\lambda f} = \frac{\lambda_0}{\lambda}

Medium     Luft     Wasser     Eis     Glas
nn     1.00     1.33     1.31     1.51

2.Die Geschwindigkeit roten Lichts in Glas ist v1 = 199,200 km.s-1 und violetten Lichts v2 = 196,700 km.s-1. Bestimme den Brechungsindex für rotes und violettes Licht. (c = 3.108 m.s-1)

Lösung:

Analyse:

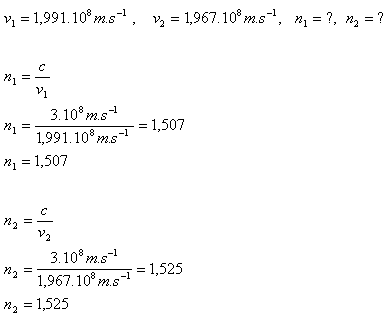
physics-reflection-and-refraction-2.gif 

Der Brechungsindex für rotes Licht in Glas ist n1 = 1.507, für violettes Licht ist er n2 = 1.525.

3.Licht trifft aus der Luft (n1 = 1) unter dem Winkel α = 680 auf die Wand eines Diamanten. Der gebrochene Strahl steht senkrecht auf dem reflektierten Strahl. Berechne:

  • den Brechungsindex des Diamanten für das verwendete Licht
  • die Lichtgeschwindigkeit im Diamanten (c = 3.108 m.s-1)

Lösung:

Analyse:

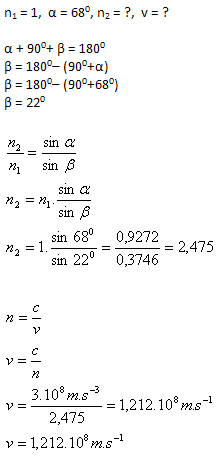
physics-reflection-and-refraction-3.gif 

  • Der Brechungsindex des Diamanten ist n2 = 2.475.
  • Die Lichtgeschwindigkeit im Diamanten ist v = 1.212·108 m.s-1.

4.Aus der Luft auf die Wasseroberfläche (n = 1.33) fallendes Licht wird unter dem Winkel β = 300 gebrochen. Bestimme den Einfallswinkel α und den Reflexionswinkel α‘.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

5.Auf dem Grund eines Sees steckt ein 1 Meter langer senkrechter Pfahl, der vollständig unter der Wasseroberfläche liegt. Bestimme die Länge seines Schattens auf dem Seegrund, wenn n1(Luft) = 1, n2(Wasser) = 1.33 und die Sonne sich in der Höhe φ = 300 über der Oberfläche befindet.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

6.

Ein Lichtstrahl trifft aus der Luft auf eine ebene Grenzfläche von Luft und Glas, wird unter einem Winkel von 600 reflektiert und gleichzeitig unter einem Winkel von 300 in das Glas gebrochen. Bestimme die Lichtgeschwindigkeit in Glas.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

7.Die Wellenlänge gelben Lichts in Luft beträgt λ0 = 590 nm. Wie groß ist die Wellenlänge des Lichts in Glas, wenn n = 1.5 ist? Berechne außerdem die Lichtgeschwindigkeit in diesem Medium.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

8.Unter welchem Grenzwinkel muss Licht einfallen, damit Totalreflexion auftritt, wenn Licht sich ausbreitet:

  • a) von Glas zu Luft (n1 = 1.5)
  • b) von Wasser zu Luft (n‘1 = 1.33)
  • c) von Glas zu Wasser n2(Luft) = 1
Bitte melden Sie sich an, um die Lösung anzuzeigen.

9.Bestimme die Dicke der Seifenblasenwand (n = 1.33), wenn weißes Licht auf sie fällt. Das Interferenzmaximum 1. Ordnung wird im grünen Licht beobachtet (fZ = 5.7·1014 Hz).

Bitte melden Sie sich an, um die Lösung anzuzeigen.

10.Am Boden eines Baches mit einer Tiefe von 32 cm liegt ein Steinchen. Ein Junge möchte es mit einem Stab berühren, den er über der Oberfläche in einem Winkel von 450 hält. In welchem Abstand vom Stein wird der Stab nach dem Eintauchen den Boden des Baches berühren? (n1=1, n2=1.33)

Bitte melden Sie sich an, um die Lösung anzuzeigen.

11. Der Brechungsindex von Eis ist n1 = 1.31, von Glas n2 = 1.51, von Öl n3 = 1.47. Wie groß ist die Lichtgeschwindigkeit in diesen Medien?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

12. Berechne den Brechungsindex eines Stoffes, wenn beim Einfall aus Luft bei einem Einfallswinkel α = 300 der Brechungswinkel β = 150 ist. Wie groß muss der neue Einfallswinkel α/ sein, wenn der Brechungswinkel β/ = 21.50 ist?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

13.Ein Lichtstrahl fällt auf einen ebenen Spiegel unter einem Einfallswinkel α = 200. Wie ändert sich der Winkel zwischen einfallendem und reflektiertem Strahl, wenn der Strahl unter einem Winkel α/ = 350 auf den Spiegel fällt?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

14.Ein Lichtstrahl tritt aus Wasser (n1 = 1.33) in Glas (n2 = 1.51) über. Entscheide, ob es sich um Brechung zum Lot hin oder vom Lot weg handelt, wenn der Einfallswinkel α = 600 ist.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

15. Um welchen Winkel hat sich ein kleiner Spiegel gedreht, wenn sich auf einer Skala im Abstand l = 150 cm vom Spiegel der Lichtstrahl von der Nullstellung – in der er senkrecht auf die Skala fällt – um h = 25 cm verschiebt?

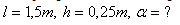
odraz-a-lom-svetla-15-1
Bitte melden Sie sich an, um die Lösung anzuzeigen.

16.Ein Lichtstrahl fällt auf einen Spiegel. Der Spiegel dreht sich um 10 um eine Achse, die in der Spiegelebene liegt und senkrecht zum Strahl ist. Um welchen Winkel wird der reflektierte Strahl abgelenkt? Um wie viel verschiebt sich der Lichtfleck auf einem Schirm, der senkrecht zum reflektierten Strahl steht und sich 5 m vom Spiegel entfernt befindet?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

17. Wie groß ist der Grenzwinkel für Licht, das auf die Grenzfläche zwischen Glas (n1 = 1.51) und Wasser (n2 = 1.33) fällt?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

18.In einer Tiefe von h = 600 mm unter der Wasseroberfläche befindet sich eine punktförmige Lichtquelle. Bestimme Form und Größe des Teils der Wasseroberfläche, durch den das Licht über die Oberfläche austritt.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

19.Der gebrochene Strahl bildet mit dem reflektierten Strahl einen Winkel von ω = 900. Bestimme den relativen Brechungsindex des Stoffes, in den der Strahl gebrochen wird, wenn sin α = 0.8 gilt.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

20. Ein Lichtstrahl fällt aus Luft (n = 1) unter einem Winkel α = 600 auf Glas. Der Brechungsindex von Glas für rotes Licht ist n1 = 1.735, für violettes n2 = 1.811. Bestimme den Winkel zwischen dem gebrochenen roten und violetten Strahl.

Bitte melden Sie sich an, um die Lösung anzuzeigen.