Redox equations
Redox equations are chemical equations of redox reactions. In redox reactions, the oxidation numbers of atoms change, therefore knowledge of chemical nomenclature and the rules for determining oxidation numbers is an essential prerequisite for successfully solving redox equations.
Reduction is the process in which an atom lowers its oxidation number. Oxidation is the process in which an atom increases its oxidation number. The change in oxidation number occurs through the actual or formal transfer of electrons (oxidation) or the acceptance of electrons (reduction; since electrons have a negative electrical charge, their acceptance lowers the oxidation number).
Reducing agent is a reactant that causes the reduction of another reactant (at least one atom of the reducing agent increases its oxidation number). Oxidizing agent is a reactant that causes the oxidation of another reactant (at least one atom of the oxidizing agent decreases its oxidation number).
Half-equation expresses only oxidation or only reduction; in electrochemistry it is also called the electrode equation.
When solving redox equations, we follow general rules for calculating stoichiometric coefficients using the following procedure:
- Determine the oxidation numbers of all atoms in the equation.
- Write the half-equation for oxidation and the half-equation for reduction.
- Adjust the oxidation and reduction half-equations mathematically so that the electron balance rule is followed.
- Add and adjust both half-equations to obtain the simplified redox equation (SRR).
- Reflect the obtained atom counts in the chemical equation using stoichiometric coefficients.
- Based on the atom balance rule, assign stoichiometric coefficients to substances containing atoms that did not change their oxidation number.
- If it is an ionic redox equation, use the charge balance rule to determine stoichiometric coefficients.
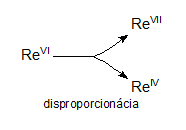
Simple disproportionation and comproportionation redox reactions are such chemical reactions in which the oxidation number of atoms of only one element changes; otherwise, they do not differ from other redox reactions.
Redox equations in which reactants contain atoms of a given element with one oxidation number and products contain atoms of the same element with different oxidation numbers are called disproportionation equations. For example:
3ReVIF6 + 10H2O → 2HReVIIO4 + ReIVO2 + 18HF
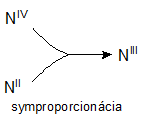
Redox equations in which reactants contain atoms of a given element with different oxidation numbers and products contain atoms of the same element with only one oxidation number are called comproportionation equations. For example:
NIVO2 + NIIO + 2NaOH → 2NaNIIIO2 + H2O
1. Balance the redox equation:
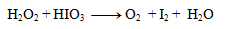
Solution:
The first step is to determine the oxidation states of the atoms in each compound:
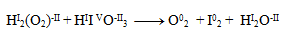
Thus, only iodine and oxygen change their oxidation numbers. We write half-reactions for them, i.e. reactions involving only the given oxidizing/reducing element and electrons.
Oxidation:
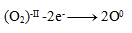
Reduction:
2IIV +10e- -------> 2I0
Next, we multiply the equations so that the number of electrons balances:
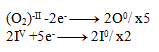
And then we add the equations:
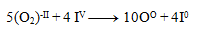
We substitute the obtained coefficients into the original equation and calculate the number of remaining atoms to comply with the law of conservation of atoms of the same element. The resulting equation has the form:
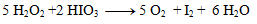
2.Complete the stoichiometric coefficients in the redox equation:
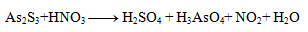
Solution:
First, it is necessary to determine the oxidation numbers of the atoms of all reactants and products:
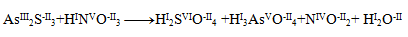
We can notice that only arsenic, sulfur and nitrogen change their oxidation numbers. For these elements we write half-reactions, in which we also indicate the number of exchanged electrons.
Oxidation equations:
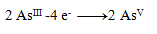
(one arsenic requires 2 electrons)
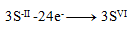
(one sulfur requires 8 electrons)
Reduction equation:
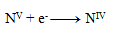
The next step is to adjust the number of exchanged electrons so that the same number is exchanged in oxidations and reductions—thus, in all three half-reactions, 28 electrons will be exchanged. 24+4=28 electrons in oxidation, so the same must occur in reduction, therefore:
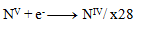
and thus
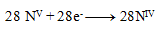
The stoichiometric coefficients from the half-reactions are added into the equation and the other elements are calculated. The resulting equation has the form:
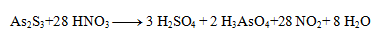
3. Balance the following redox equations:
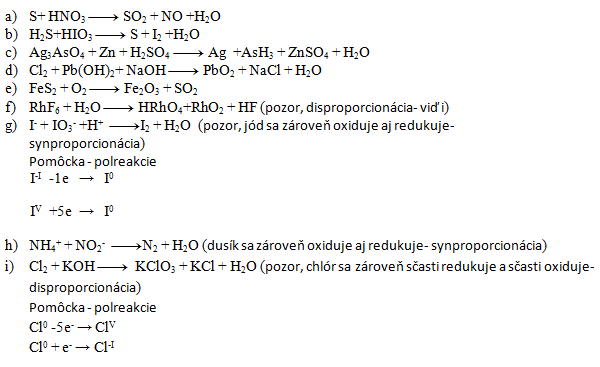
Solution:
- a) 3,4,3,4,2
- b) 5,2,5,1,6
- c) 2,11,11,6,2,11,8
- d) 1,1,2,1,2,2
- e) 4,11,2,8
- f) 3,10,2,1,18
- g) 5,1,6,3,3
- h) 1,1,1,2
- i) 3,6,1,5,3
4.Determine the stoichiometric coefficients in the following chemical equation:
Cr + H2SO4 → Cr2(SO4)3 + H2
5. Determine the stoichiometric coefficients in the following chemical equation:
Ca3(PO4)2 + SiO2 + C → P4 + CaSiO3 + CO
6.Find the stoichiometric coefficients in the following chemical equation:
MnO4– + Fe2+ + H3O+ → Mn2+ + Fe3+ + H2O
7. Find the stoichiometric coefficients in the following chemical equation:
Cu + HNO3 → Cu(NO3)2 + NO2 + H2O
8. Find the stoichiometric coefficients in the following chemical equation:
KMnO4 + HBr → Br2 + MnBr2 + KBr + H2O
9. Find the stoichiometric coefficients in the following chemical equation:
ReF6 + H2O → HReO4 + ReO2 + HF
10.Determine the stoichiometric coefficients in the following chemical equation:
MnO42– + H3O+ → MnO4– + MnO2 + H2O
11. Determine the stoichiometric coefficients in the following chemical equation:
NO2 + NO + NaOH → NaNO2 + H2O
12. Find the stoichiometric coefficients in the following chemical equation:
I– + IO3– + H3O+ → I2 + H2O
13. Find the stoichiometric coefficients in the following chemical equation (More challenging problem for a chemistry olympiad):
FeS2 + O2 → Fe2O3 + SO2
14. Find the stoichiometric coefficients in the following chemical equation (More challenging problem for a chemistry olympiad):
Au + KCN + O2 + H2O → K[Au(CN)2] + KOH