Geometric meaning of derivation
1.What is the geometric meaning of the derivative?
Solution:
Using the derivative of the function y = f(x) we can write the equation of the tangent or the equation of the normal to the graph of the function at the point T [xT , yT]
Equation of the Tangent Line:
Equation of the Normal Line:
Point T [x_T, f(x_T)] is the common point of the tangent (or normal) with the graph of the function.
Subtangent and Subnormal:
The tangent, the normal, and the x-axis form a right triangle Δ ABT (right angle at vertex T).
It holds:
-
Point T lies on line t,
-
Point A lies on line t ∩ x-axis,
-
Point B lies on line n ∩ x-axis.
-
Point T₁ [x_T; 0] is the orthogonal projection of point T onto the x-axis.
Subtangent Sₜ is the length of segment :
Subnormal Sₙ is the length of segment :
Length of the Tangent Segment TA = t:
Length of the Normal Segment TB = n:
2. Write the equation of the tangent and the equation of the normal to the curve:
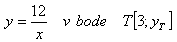
Solution:
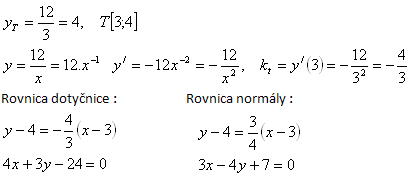
equation of tangent equation of normal
3. Write the equation of the tangent and the equation of the normal to the curve:
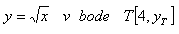
Solution:

equation of tangent equation of normal
4. Write the equation of the tangent and the equation of the normal to the curve:
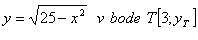
5. Write the equation of the tangent and the equation of the normal to the curve:
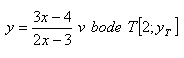
6. Write the equation of the tangent and the equation of the normal to the curve y = ln(x+1) at the point T[0; yT]
Please log in to view the solution.
7. Write the equation of the tangent to the curve y = sin 2x at the point T [3π/4 ; yT].
Please log in to view the solution.
8. Write the equation of the tangent to the curve y = x2 – 4x + 3 , which makes an angle φ = 450 with the x-axis.
Please log in to view the solution.
9. Find the equation of the tangent to the curve y = x2 - 2x + 3 , if the tangent is parallel to the line p : 3x - y + 5 = 0.
Please log in to view the solution.
10.The function is given f : y = x3 - 9x2 + 15x + 3. Determine the contact points of the horizontal tangents.
Please log in to view the solution.
11. Determine the angle φ between two tangents of the curve if one has contact point T1[3; yT1] and the other T2[-3; yT2]. The equation of the curve:
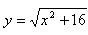
12. Determine the lengths of the subtangent, subnormal, tangent and normal to the graph of the function at the point T[1; yT]. The function has the equation:
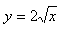
13. Calculate the lengths of the subtangent, subnormal, tangent and normal to the graph of the function y = 2x at the point T [1; yT].
Please log in to view the solution.