Pyramid and Cone


1. Characterize the calculation of volume and surface area for:

  • pyramid
  • truncated pyramid
  • cone
  • truncated cone

Solution:  

Pyramid (Sₚ = base, v = height, Q = lateral surface area)

V=13Sp⋅v,S=Sp+QV = \frac{1}{3} Sₚ \cdot v, \quad S = Sₚ + Q

Truncated pyramid (Sₚ₁, Sₚ₂ = lower and upper base, v = height, Q = lateral surface area)

V=13v(Sp1+Sp2)2,S=Sp1+Sp2+QV = \frac{1}{3} v ( \sqrt{Sₚ₁} + \sqrt{Sₚ₂})^2, \quad S = Sₚ₁ + Sₚ₂ + Q

Cone (r = base radius, v = height of the solid, s = slant height, Q = lateral surface area)

V=13πr2v,S=πr(r+s),Q=πrsV = \frac{1}{3} \pi r^2 v, \quad S = \pi r (r + s), \quad Q = \pi r s

Truncated cone (r₁, r₂ = radii of the bases, v = height of the solid, s = slant height)

V=13πv(r12+r1r2+r22),S=π(r12+r22)+Q,Q=πs(r1+r2)V = \frac{1}{3} \pi v (r₁^2 + r₁ r₂ + r₂^2), \quad S = \pi (r₁^2 + r₂^2) + Q, \quad Q = \pi s (r₁ + r₂)

2. A regular square pyramid is given (the base is a square with side a).

Fill in the missing values of the table.

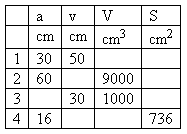
pyramid-cone-2

Solution:

For wall height apply: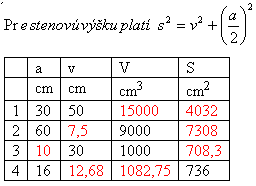
pyramid-cone-2r

3. Above each face of a cube with edge a = 30 cm, a regular square pyramid with height 15 cm is constructed.

Calculate the volume of the solid formed in this way, if the vertices of the pyramids:
a) lie outside the cube
b) lie inside the cube
Solution:

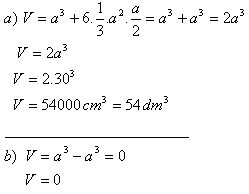
pyramid-cone-3

The volume of the solid in the first case is V = 54 dm3, in the second case it is zero.

4. Calculate the volume of a pyramid whose lateral edge of length 5 cm forms an angle α = 60° with the square base. (Angle α is the angle between the edge and the diagonal of the base.)

Please log in to view the solution.

5. Determine the mass of a concrete pillar (ρ = 2.2 g.cm-3) in the shape of a regular square frustum of a pyramid, if its square bases have sides a = 45 cm, b = 25 cm, and the height of the pillar is v = 33 cm.

Please log in to view the solution.

6. A cone with dimensions given in the table is given.

Fill in the table.

pyramid-cone-6
Please log in to view the solution.

7. A right triangle with legs a = 3 cm, b = 4 cm rotates around the longer leg.

Calculate the volume and surface area of the cone formed.
Please log in to view the solution.

8. The surface area of a cone is S = 235.5 cm2. The axial section of the cone is an equilateral triangle.

Calculate the volume of the cone.
Please log in to view the solution.

9. The lateral surface of a cone, developed into the plane, has the shape of a circular sector with central angle α = 150° and area S = 523.4 cm2.

Calculate the dimensions of this cone and its volume.
Please log in to view the solution.

10. The surface area of a frustum of a cone is 7693 cm2, the radii of the bases are 28 cm and 21 cm.

Calculate the height of the cone and its volume.
Please log in to view the solution.

11. The volume of a frustum of a cone is V = 38 000π cm3. The radius of the lower base is 10 cm larger than the radius of the upper base.

Determine the radii of the bases, if v = 60 cm.
Please log in to view the solution.

12. A frustum of a cone with radii x = 15 cm, y = 13 cm and height v = 9 cm was rolled out into a cylinder with radius r = 7.67 cm.

What is the length of this cylinder?
Please log in to view the solution.