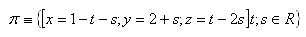Equation of a plane
1. In what way is a plane in space determined?
Solution:
A plane in space is determined by three distinct points A, B, C that do not lie on the same line.

2.Write the general equation of the plane that contains point A [-1;5;0]. Does the plane ρ pass through the origin? The normal vector of the plane is
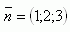
Solution:
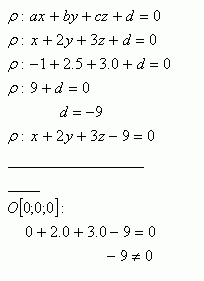
The plane x + 2y + 3z - 9 = 0 does not pass through the origin.
3. In plane ρ lie three points A[2 ; -4; 5], B[3; -1;4], C[0; -10; 7]. Write the parametric representation of this plane.
Solution:
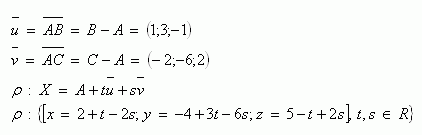
4.The plane ρ is given by parametric equations. Convert them to the general equation of the plane.
Please log in to view the solution.
5. Write the equation of plane σ that passes through point A [3;4;-5] and is parallel to the vectors
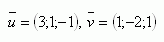
6.Write the equation of the plane that passes through points A [2;-4;5], B [3;-1;4], C [0;1;6]
Please log in to view the solution.
7. Write the equation of the plane given by two parallel lines:
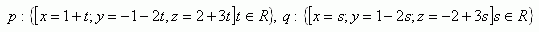
8.Write the general equation of the plane τ that is parallel to the x-axis and passes through points A[-2;-1;-3], B [2;3;0]
Please log in to view the solution.
9. Write the equation of plane π that passes through point M[-4;0;4] and intercepts on the coordinate axes segments p = 4, q = 3.
Please log in to view the solution.
10. Given the plane ρ : 2x - 2y + z - 6 = 0. Calculate the angles between its normal and the x, y, z coordinate axes.
Please log in to view the solution.
11.Determine whether point A [22;2;–5] lies in the plane
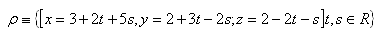
12.Determine the coordinate "x" of point M [x;1,2] so that point M lies in the plane
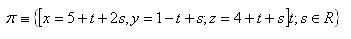
13.Write the general equation of the plane that passes through point A and is perpendicular to segment AB, given:
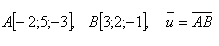
14.Write the general equation of the plane τ that intercepts on the coordinate axes segments p = 2, q = 1, r = 5.
p = 2, q = 1, r = 5.
15.Write the equation of plane π that passes through point M and is perpendicular to line p. Solve for the given data:
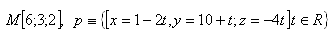
16.Show that points A, B, C, D lie in a single plane. Solve for:
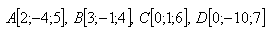
17.Given three spheres π, τ, ρ. Write the general equation of the plane χ that passes through the centers of these spheres. It holds that:
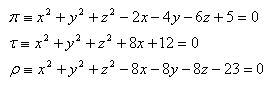
18.Write the general equation of plane π that passes through the points
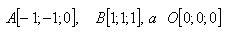
19.Convert the parametric form of plane μ to the general form, given
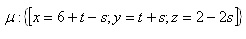
20.For which value of the parameter "m" from the set R does point M[0;6;m] lie in the plane