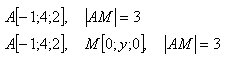Line in space
1. What do we know about the properties of a line in space?
Solution:

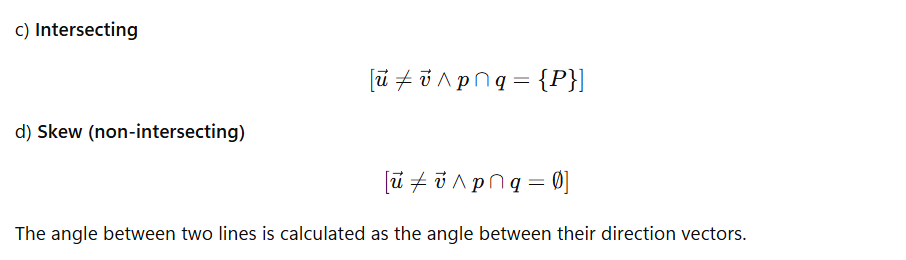
2. Write the parametric equation of the line that passes through point A [2;4;-3], parallel to line BC, where B [3;2;-1], C [7;1;9]. Determine which of the points M [-1;2;0], N [6;3;7] lies on this line.
Solution:

The point N [6;3;7] lies on line p.
3. Line p is parallel to line AB if A [4;-7;2], B [-1;3;6]. Determine Yc and Zc so that the point C [2;Yc;Zc] also lies on this line.
Solution:
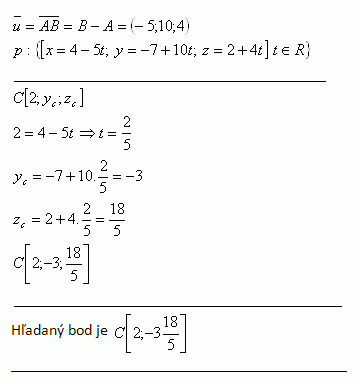
4. Given triangle ΔABC with vertices A [-2;5;4], B [2;3;-1], C [2;7;-2]. Write the parametric equations of the sides of the triangle a = BC, b = AC, c = AB
Please log in to view the solution.
5. Given point M [3;2;-1] and the parametric equation of line p
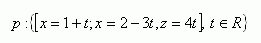
Write:
a) the equations of line q that passes through point M and is parallel to p
b) the equations of line q that passes through point M and is perpendicular to p
c) the equations of line q that is parallel to the y-axis
6. Determine the mutual position of the lines whose parametric equations are
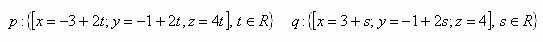
7. Two lines p and q are given. Determine their mutual position. If they intersect, find their intersection point and the angle between them.
Please log in to view the solution.
8. Determine the mutual position of lines p and q, their intersection point and the angle they form. Also calculate the distance from point M [5;-1;4] to the intersection of the lines.
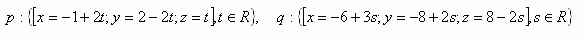
9. Decide which of the points A, B lies on line p, if it holds
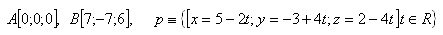
10. Write the parametric equation of the line that passes through points A [3;-7;2], B [5;-4;1] and determine the coordinates x, z of point C [x;2;z] so that it lies on line p.
Please log in to view the solution.11. Determine the mutual position of lines p and q in space if:
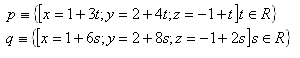
12. Determine the mutual position of lines p and q in space if:
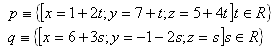
13. Determine the angle (inclination) between lines p and q in space if:
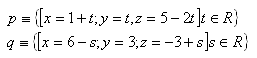
14. Determine the angle between lines p and q in space if:
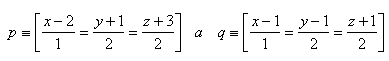
15. Given points A, B, C. Write the parametric equation of line p that passes through the midpoints of segments AB and BC. Solve for the points:
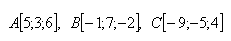
16. Calculate the distance from point M to line p, if:
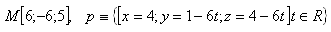
17. Given lines p and q. Find a vector that is perpendicular to both direction vectors of the given lines. Solve for the lines:
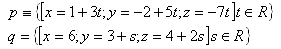
18. Given lines p and q. Determine "m" so that the lines are non-parallel (intersecting). Determine their intersection.
Solve for the lines:
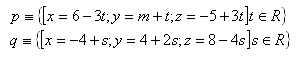
19. Calculate the distance from point M to the intersection of lines p and q. Solve for point M [2;3;–23] and the lines:
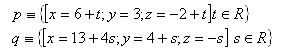
20. Given point A [-1;4;2]. On the y-axis determine point M such that |AM| = 3. Also write the parametric equation of line AM.