Line in a plane
1. Explain the different types of line equations in a plane.
- parametric form
- general form
- slope-intercept form
- distance from a point to a line
Solution:
a) Parametric form:

2. Write the equation of the line passing through points A[2;7] and B[5;1] in the form:
b) general
c) slope-intercept
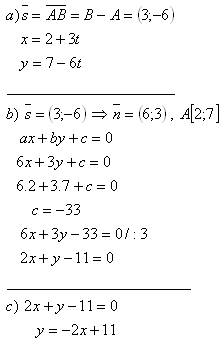
3. Write the equation of the line on which the midpoint of segment AB lies, if A[1;5] and B[7;3].
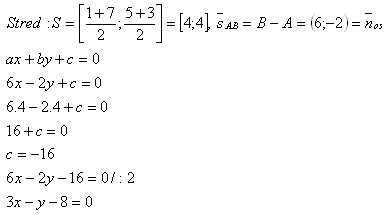
4. Write the equation of the line on which the altitude vc lies in triangle A[5;6], B[-2;4], and C[6;-1].
Please log in to view the solution.5. The line (2–m)x + 3my + (2m-6) = 0 is given.
a) the line passes through the origin
b) the line is parallel to the x-axis
c) the line is parallel to the y-axis
6. The line is given by p: 4x – 3y +6 = 0
b) convert it to parametric form
c) calculate the distance from the point not on the line to the line
7. Write the equation of a line parallel to line p: 5x +12y -1 = 0 and at a distance d = 5 units from it.
Please log in to view the solution.8. The triangle has vertices A[-1;-5], B[9;-1], and C[1;7].
a) equation of side c = AB
b) equation of median tc
c) equation of altitude to side c, vc
9. Write the equation of the line that makes an angle φ = 135° with the x-axis and passes through point A[3;-1].
10. A light beam originates from source A[-1;-5], reflects on the x-axis like from a mirror, and passes through point B[9;-5].
11. The vertices of a triangle A and B and the intersection of the altitudes Q are given. Determine the coordinates of the triangle's vertex C if
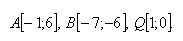
12. On line p, find point C, which is equidistant from points A and B.
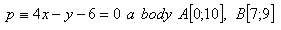
13. Calculate the length of altitude va in triangle ABC if its sides have the equations
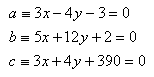
14. Opposite sides of square ABCD lie on parallel lines
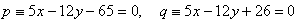
Calculate the perimeter and area of this square.
15. Determine the perimeter and area of the right triangle cut by the line 3x + 4y –12 = 0 on the coordinate axes.
Please log in to view the solution.
16. Write the equation of a line parallel to 5x + 12y -1 =0 and at a distance d = 5 from it.
Please log in to view the solution.
17. Calculate the distance from point A[2;-4] to the line 3x + 4y = 0.
Please log in to view the solution.
18. The diagonals of a rhombus u1 = 4, u2 = 6 lie on the coordinate axes (u1 on the x-axis). Write the equations of the lines on which the sides of the rhombus lie.
Please log in to view the solution.
19. Determine the equation of a line passing through point [2;3] such that the segment on the x-axis is half the length of the segment on the y-axis.
Please log in to view the solution.
20. Given points A[3;-2], B[1;4], C[-1;-3]. Determine point D so that line CD intersects segment AB at its midpoint S and CD = 3·|CS|.
Please log in to view the solution.