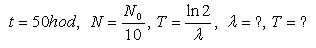Logarithms - Basics
Logarithm
Logarithm of a positive number x to the base a ( a is a positive number not equal to 1 ) is the power y to which the base a must be raised in order to produce the number x.
logax =y because ay=x a > 0 and a ≠ 1
Logarithms properties:
a.) logarithm of a product:
b.) logarithm of a quotient:
c.) logarithm of a power:
1. Rewrite to logarithm notation:
102 = 100 log10 100 = 2
45 =1024 log41024 = 5
130 = 1 log131 = 0
10-3 = 0,001 log100,001 =-3
640,5 =8 log648 = 0,5
5-2 = 0,04 log50,04=-2
2. Solve and give a reason:
log101000 log101000 = 3 because 103 = 1000
log381 log381 = 4 because 34 = 81
log20,5 log20,5 =-1 because 2-1 = 0,5
log171 log171 = 0 because 170 =1
log1111 log1111 = 1 because 111 = 11
log50,2 log50,2 = -1 because5-1 = 0,2
log150 log150 =
log5(-25) log5(-25) = n0
log0,40,4 log0,40,4 = 1 because 0,41 =0,4
log149 log149 = 0 undefined
3. Determine x:
log2x = 3 x = 23 =8
log10x = -4 x = 10-4 = 0,0001
log16x = 0,5 x =160,5= 4
log20x =1 x = 201=20
log25x = -0,5 x =25-0,5 = 0,2
log0.2487x = 0 x =0,24870 =1
4. Determine a:
loga25 =2 a = 5
loga81 = 4 a = 3
loga100000 =5 a = 10
loga512 = 3 a = 8
loga0,01 = -2 a = 10
loga5 = 0,5 a = 25
loga36 = 2 a = 6
loga64 = 1 a = 64
5. Logarithmize following expressions (to the base a)
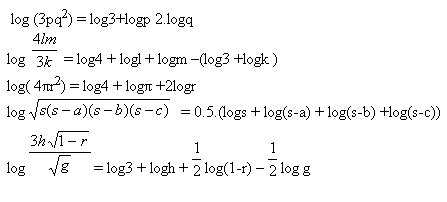
6. Determine x:
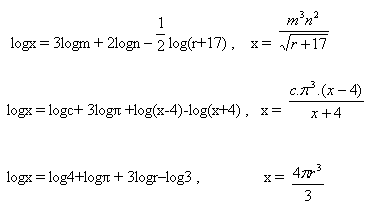
7. Enumerate the expression:
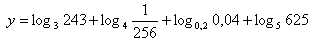
Solution:
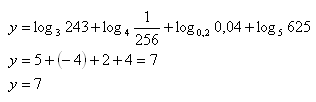
Reason:
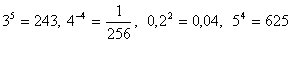
8. Logarithmize the expression (to the base a):
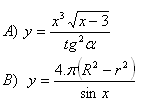
Solution:

9. Enumerate the expression:
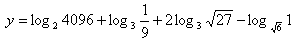
Solution:
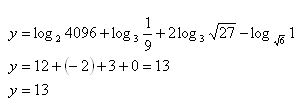
Reason:
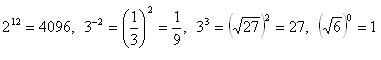
10. Enumerate the expression:
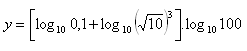
11. Use the decadic logarithm to solve the equation:
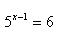
12.Use the decadic logarithm to solve the equation:
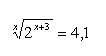
13.Use the decadic logarithm to solve the equation:
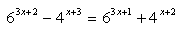
14.During t = 50 hours the activity of radioactive sodium lowers to 1/10 of the initial value. Determine the half life of the nuclide using a natural logarithm.