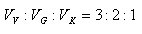Evidence
1. How do we prove the truth of a mathematical statement?
Solution:


2.Prove the statement by direct proof:
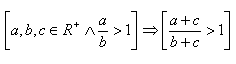
Solution:
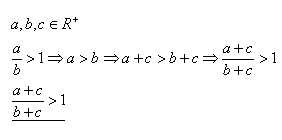
What holds according to the assumption.
3.Prove the statement by direct proof:
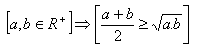
Solution:
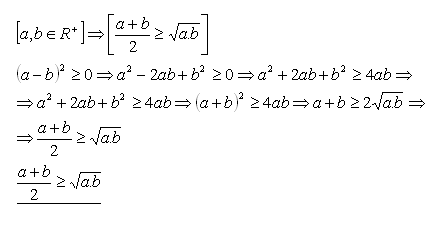
It holds for all a, b ∈ R+
4.Prove the statement by direct proof:
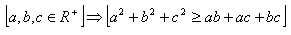
5.Prove the statement by direct proof:
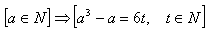
6.Prove the statement by indirect proof: If a2 is a natural number divisible by 3, then a is a natural number divisible by 3.
Please log in to view the solution.
7.Prove the statement by indirect proof: for a natural number a it holds: If a4 + 2 is not divisible by 3, then a is divisible by 3.
Please log in to view the solution.
8.Prove by contradiction the statement: For all positive real numbers a, b it holds that:
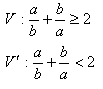
9.Prove by contradiction: The number √3 is irrational
Please log in to view the solution.
10.Using mathematical induction, prove the statement: For all natural numbers n it holds that:
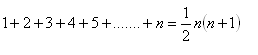
11.Using mathematical induction, prove the statement: For all natural numbers n it holds that:
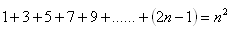
12.Using mathematical induction, prove the statement: For every natural number n it holds that:
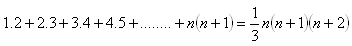
13. Using mathematical induction, prove the statement: For every natural number n it holds that:
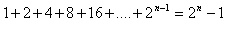
14.Using mathematical induction, prove the statement:
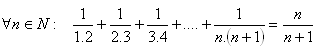
15.Using mathematical induction, prove the statement:
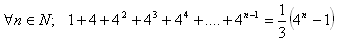
16.Using mathematical induction, prove de Moivre’s theorem
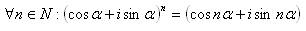
17.Inside triangle ΔABC a point U is given. Prove that the following relation holds
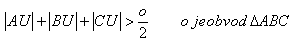
18.Prove the statement: A triangle’s median is less than half of the perimeter.
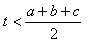
19.Prove the statement:
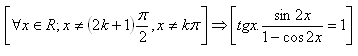
20.A sphere and a cone are inscribed in an equilateral cylinder. The base of the cone coincides with the base of the cylinder, the vertex of the cone is at the center of the other base. Show that Archimedes’ result holds. (Archimedes approx. 287–212 BC)