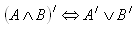Statements
1.Characterize the basic properties of statements.
Solution:
A statement is any declarative sentence for which it makes sense to consider whether it is true or false. We denote statements by: A, B, C, D, P, ... etc.
Statement
- a) true – “holds,” has the truth value (1)
- b) false – “does not hold,” has the truth value (0)
Negation of a statement
For every statement A, we can form a statement A‘ that denies (negates) what statement A asserts. Statement A‘ is called the negation of statement A. We form the negation by putting before the statement a prefix like “not ...,” “is not,” or the text “it is not true that ....”
| A | A‘ |
| (1) | (0) |
| (0) | (1) |
2.Create negations for the given statements. Determine the truth values of the original and negated statements.
A: The number 3 is a prime number (1)
B: Bratislava lies in Egypt (0)
C: Prešov Region
D: Mathematics is a science (1)
E: The number 22 is divisible by 2 (1)
F: Good day!
G: The abominable snowman Yeti exists
H: Sine of 300 is –2.1 (0)
I: Do you have homework?
J: x2 - 5x + 6 = 0
K: The number 2574364 is divisible by 4 (1)
L: It holds that (a + b)2 = a2 + b2 (0)
M: The area of a circle is S = π·r2 (1)
N: 42 equals 18 (0) equals 18 (1)
O: I have a new car (1)
P: He/She is not here.
Solution:
A': The number 3 is not a prime number (0)
B': Bratislava does not lie in Egypt (1)
C : not a statement
D': Mathematics is not a science (0)
E': The number 22 is not divisible by 2 (0)
F : not a statement
G : cannot be decided
H': Sine of 300 is not −2.1 (1)
I : not a statement
J : not a statement
K': The number 2574364 is not divisible by 4 (0)
L': It is not true that (a + b)2 = a2 + b2 (1)
M': The area of a circle is not S = π·r2 (0)
N': It is not true that 42 equals 18 (1)
O': I do not have a new car (0)
P : not a statement
3.Let’s review the properties of a quantified statement.
Solution:
A quantified statement is a declarative sentence that gives a certain number, or an estimate of the number, of objects, persons, etc., with the same property. In a quantified statement we encounter words such as: exactly, at most, every, all, some, at least, none ... etc., which are called quantifiers, as well as numerals.
- The statement “at least 5” means 5 or more.
- The statement “at most 5” means 5 or less.
For symbolic notation of quantified statements we use
- a) the universal quantifier
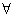 – “for every (all) it holds that.....”
– “for every (all) it holds that.....” - b) the existential quantifier
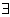 – “there exists at least one ... for which it holds that ....”
– “there exists at least one ... for which it holds that ....”
Negation of a quantified statement
| Statement | Negation of the statement |
| Every ... is ... | At least one ... is not ... |
| At least one ... is ... | Every ... is not ... |
| At least n ... are ... (n>1) | At most (n−1) ... are ... |
| At most n ... are ... (n>=1) | At least (n+1) ... are ... |
| Exactly n ... are ... | At most (n−1) or at least (n+1) ... are ... |
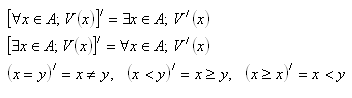
4. Negate the following statements:
A: The number 3 is a root of the equation x2 = 9 (1)
B : 23 − 5 > 7 (0)
C: The diagonals of a square are perpendicular to each other (1)
D: 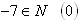
E: Every problem has a solution (0)
F: There exists at least one rectangle whose diagonals are perpendicular (0)
G: There exists at least one right triangle (1)
H: This book has at most 50 pages (1)
I: Every song has an ending (1)
J: There were exactly 20 parents at the PTA meeting (0)
K: 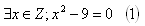
L: 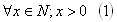
5. What do we know about compound statements?
Please log in to view the solution.
6.Negate the following statements:
A: Peter and Mária will come
B: It is raining and it is wet
C: The sun is shining or the wind is blowing
D: If we get angry, we will be bad
E: If Jozef comes, then Eva will come as well
F: I am in a good mood if and only if it is raining
G: Every trapezoid is equilateral
H: There exists at least one prime number that is even
I: In class 1.A at least 8 students wear glasses
J: 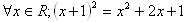
7. From the given statements A, B create:
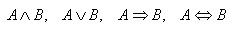
8.Given the statements P: it is raining, S: the Sun is shining, V: the wind is blowing. Create compound statements from them
Please log in to view the solution.
9.Determine using a truth table the truth value of the formula: