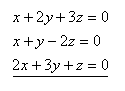Matrix
1. What are the basic properties of matrices.
Solution:
A rectangular scheme of m, n real numbers arranged into m rows and n columns is called a matrix (of type m,n). If m = n, it is a square matrix of degree n. The numbers a11, a32, ... amn are called elements of the matrix.
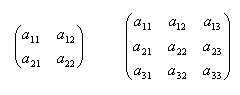
Zero matrix: Identity matrix:
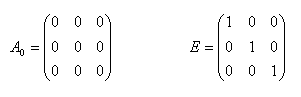
Inverse matrix A–1: 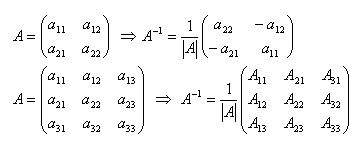
Sum of matrices A + B
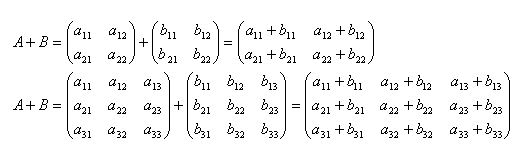
2. Explain the procedure for multiplying two matrices.
Solution:
The product of two matrices only makes sense if the left matrix has as many columns as the right matrix has rows. Such matrices are called “conformable.”
The product of matrices is not commutative!
Multiplication of a matrix by a number: 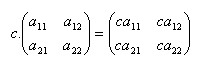
Product of matrices A.B
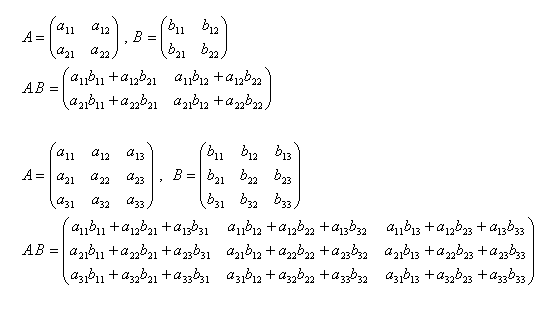
3.Add matrices A+B and M+N if
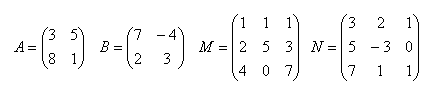
Solution:
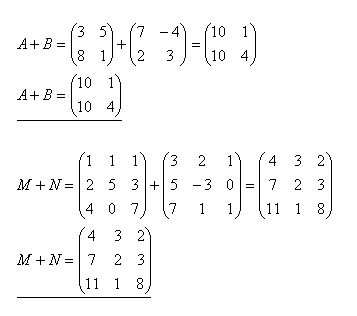
4.Multiply matrices A.B and C.D if
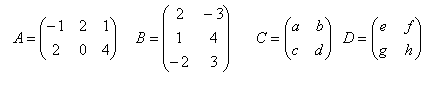
5.Show that the product of matrices is not commutative.
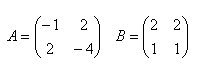
6.Given matrix A. Find the matrix A2 if
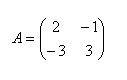
7.Given matrix B. Find the matrix B2 if
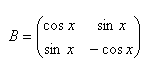
8.Find the product of matrices A.B if
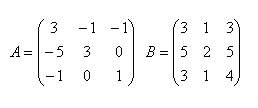
9.Explain the procedure for calculating the inverse matrix A–1 from matrix A.
Please log in to view the solution.
10.For matrix A, find the inverse matrix A–1 and check if
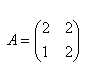
11.For matrix A, find the inverse matrix A–1 and check if
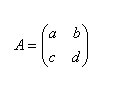
12.Calculate the inverse matrix A–1 for matrix A, if
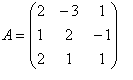
13.Calculate the inverse matrix A–1 for matrix A and check (see example 12), if
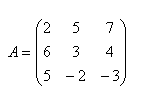
14.Solve the matrix equation A + X = B if
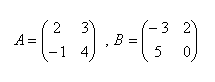
15.Calculate matrix X from the equation 2A + 3X = B if
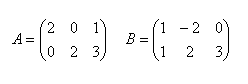
16.Solve the matrix equation A.X = B and check if
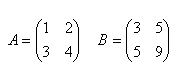
17.Solve the equation A.X = B and check if
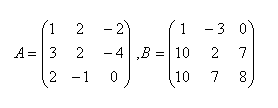
18.Explain the procedure for solving a system of linear equations using the inverse matrix.
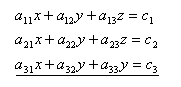
19.Using the inverse matrix, solve the system of equations:
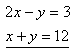
20.Using the inverse matrix, solve the system of equations:
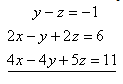
21.Using the inverse matrix, solve the system of equations:
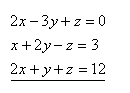
22.Using the inverse matrix, solve the system of equations:
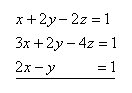
23.Explain the concept of the “rank of a matrix” and the conditions for solving a system of linear equations by the Gauss method.
Please log in to view the solution.24.Solve the system of equations by the Gauss method:
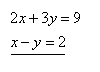
25.Solve the system of equations by the Gauss method:
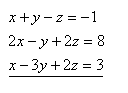
26.Solve the system of linear equations using the Gauss method:
2x – y + z = 3
3x + y – z = 5
27.Solve the system of equations by the Gauss method: