Sets


1. Explain the concept of a set and set operations.

Solution:

A set is a collection of material objects (objects, people, numbers, etc.)
which we call elements. A set is given when, for any object, we can decide whether it belongs to the set or not.
We denote sets by capital letters A, B, M, Q, R…
Elements in a set are denoted by lowercase letters a, b, x, y, …

A={2; −5; 73; x},−5∈A,y∉AA = \{2;\,-5;\,\tfrac{7}{3};\,x\},\quad -5 \in A,\quad y \notin A

Determining a set

a) By listing all its elements

A={1,2,3,4,5,6,7}A = \{1, 2, 3, 4, 5, 6, 7\}

b) By specifying a common property of the elements that belong to the set

A={x∈N; x≤7}A = \{x \in \mathbb{N};\ x \leq 7\}

Set operations

Complement of a set A is all elements of set M that do not belong to set A

A′={x∈M; x∉A}A' = \{x \in M;\ x \notin A\}

Intersection of two sets A and B is all elements of set M that belong to both A and B at the same time

A∩B={x∈M; x∈A and x∈B}A \cap B = \{x \in M;\ x \in A \ \text{and} \ x \in B\}

Union of two sets A and B is all elements of set M that belong to A or to B (they may belong to both)

A∪B={x∈M; x∈A or x∈B}A \cup B = \{x \in M;\ x \in A \ \text{or} \ x \in B\}

Difference of two sets A – B is all elements of set M that belong to A and do not belong to B

A−B={x∈M; x∈A and x∉B}A - B = \{x \in M;\ x \in A \ \text{and} \ x \notin B\}

Subset relation:
Set B is a subset of set A if all elements of B belong to A

B⊆A ⟺ (∀x∈M; x∈B⇒x∈A)B \subseteq A \iff (\forall x \in M;\ x \in B \Rightarrow x \in A

2. List all elements of the following sets:

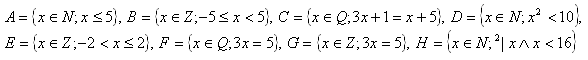
mnoziny-2z.gif

Solution:

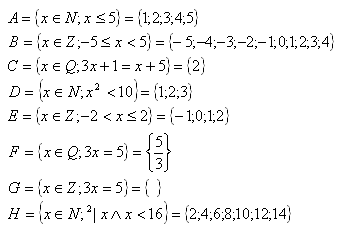
mnoziny-2r.gif

3. The following sets are given:

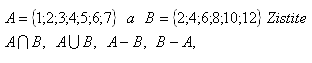
mnoziny-3z.gif

Solution:

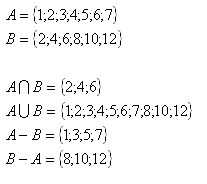
mnoziny-3r.gif

4. The following sets are given:

mnoziny-4z.gif
Please log in to view the solution.

5. The following sets are given:

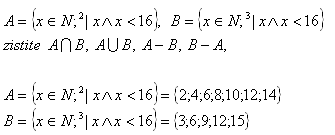
mnoziny-5z.gif
Please log in to view the solution.

6. Represent the given sets as intervals:

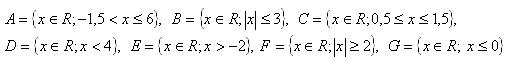
mnoziny-6z.gif
Please log in to view the solution.

7. The following intervals are given:

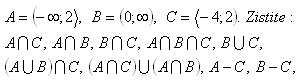
mnoziny-7z.gif
Please log in to view the solution.

8. Explain how to calculate the number of elements in finite sets.

Please log in to view the solution.

9. At the embassy reception, everyone speaks at least one foreign language. 15 people speak English, 12 speak German, and 7 speak both languages. How many people are there in total if no one speaks any other languages?

Please log in to view the solution.

10.Out of 35 students, 8 subscribe to the SME daily, 10 to Pravda, and 21 students do not subscribe to any of these newspapers. How many students subscribe to both newspapers?

Please log in to view the solution.

11.In one day, the auto repair shop fixed 24 brake problems and 36 engine problems on 46 cars. How many cars had only brake problems and how many only engine problems?

Please log in to view the solution.

12.A survey of reading interests showed that 60% of students read magazine A, 50% magazine B, 50% magazine C, 30% both A and B, 20% both B and C, 30% both A and C, and 10% all three magazines. What percentage of students read exactly two magazines and what percentage read none of these magazines?

Please log in to view the solution.

13.Use Venn diagrams to illustrate the sets:

mnoziny-13z.gif
Please log in to view the solution.