Electromagnetic waves

1. Characterize the nature and properties of electromagnetic waves.

Solution:

Every change in the magnetic field induces a varying electric field. Every change in the electric field induces a varying magnetic field. The magnetic and electric fields always exist simultaneously and form an electromagnetic field, which propagates through space at a speed of c = 3.10⁸ m.s^-1.

Phase velocity of electromagnetic wave is:

v = \frac{1}{\sqrt{\varepsilon \mu}}

A progressive electromagnetic wave is characterized by the equation:

u = U_m \sin \left(2\pi\left(\frac{t}{T} - \frac{x}{\lambda}\right)\right), \quad \lambda = cT = \frac{c}{f}

i = I_m \sin \left(2\pi\left(\frac{t}{T} - \frac{x}{\lambda}\right)\right), \quad x = \text{distance from source}

A dipole (radiator, antenna) is an open oscillating LC circuit that emits (receives) electromagnetic waves.

Half-wave radiator:

l = \frac{\lambda}{2} = \frac{c}{2f}

Electromagnetic wave does not propagate along the conductors but arises between the conductors.

Two conductors can be connected:

Short-circuited – at the end of the line a conductor is connected; there is zero voltage and a current antinode.
Open-circuited – at the end of the line no conductor is connected; there is a voltage antinode and a current node.

The interference of the original and reflected wave arises between the conductors → “standing electromagnetic wave”

Amplitudes of standing electromagnetic wave:

	$R$ $λ$	Voltage	Current
Short-circuited	$R \to 0$ , $\lambda$	$U_0 = 2U_m \sin \frac{2\pi x}{\lambda}$	$I_0 = 2I_m \cos \frac{2\pi x}{\lambda}$
Open-circuited	$R \to \infty$ , $\lambda$	$U_0 = 2U_m \cos \frac{2\pi x}{\lambda}$	$I_0 = 2I_m \sin \frac{2\pi x}{\lambda}$

2.Characterize the individual types of electromagnetic radiation.

Radio radiation
Microwaves
Infrared radiation
Visible light
Ultraviolet radiation
X-ray radiation
Gamma radiation
Cosmic radiation

Solution:

Radio radiation:

f = 10^{5}\,\text{Hz} – 10^{9}\,\text{Hz}, \; (\lambda = 10^{2}\,\text{m} – 10^{-1}\,\text{m})

Used for sound and image transmission – radio, television, radar.

Microwaves: $f = 10^{9}\,\text{Hz} – 10^{12}\,\text{Hz}, \; (\lambda = 10^{-1}\,\text{m} – 10^{-4}\,\text{m})$
Thermal vibrations of atoms and molecules.

Infrared radiation: $f = 10^{12} Hz– 10^{14} Hz, (λ = 10^{- 4} m– 10^{- 5} Hz)$
Sources are warm bodies – the Sun, heated metal, etc. Used as a heat source, in microwaves, remote controls, photography in the dark.

Visible light: $f = 3.8 \cdot 10^{14} Hz– 7.8 \cdot 10^{14} Hz, λ = 7.9 \cdot 10^{- 7} m– 3.86 \cdot 10^{- 7} m$

Ultraviolet radiation: $f = 10^{15} Hz– 10^{16} Hz, (λ = 10^{- 7} m– 10^{- 8} m)$
The Sun, mercury vapor lamps, electric arcs. Causes tanning of the skin, kills bacteria, at high doses causes skin cancer. Used in so-called “mountain sunlamps.”

X-ray radiation: $f = 10^{16} Hz– 10^{20} Hz, (λ = 10^{- 8} m– 10^{- 12} m)$
Produced when cathode rays strike an anode target. Used in medicine for diagnosis.

Gamma radiation: $f = 10^{20} Hz– 10^{24} Hz, (λ = 10^{- 12} m– 10^{- 16} m)$
Very strong penetrating radiation; at small doses it treats cancer, at high doses it arises from nuclear explosions, decay of atomic nuclei, and atomic bombs.

Cosmic radiation: $f = 10^{24} Hz \Rightarrow (λ = 10^{- 16} m)$
A stream of protons or photons falling to Earth from space.

3.Calculate the speed of electromagnetic waves in a vacuum and in water, given that for water ε_r=81, μ_r = 1.

Solution:

Analysis:

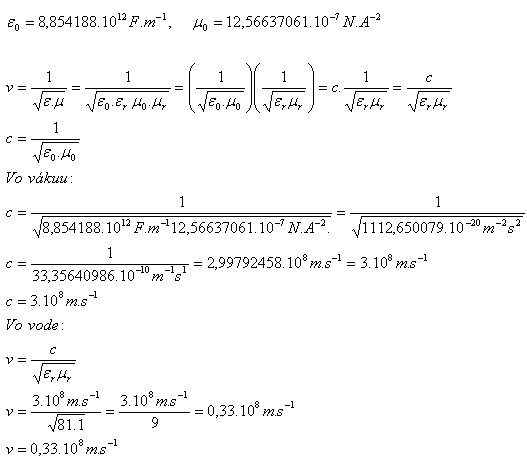
The speed of electromagnetic waves in a vacuum is c = 3.10⁸ m.s^-1, and in water v = 0,33.10⁸ m.s^-1.

4.The VHF radio communication band has a frequency range of 66 MHz to 73 MHz. Determine the smallest and largest wavelength of electromagnetic waves in this band.

Electromagnetic waves

Register and unlock all the solutions!