Stability of bodies
1. What do we understand by the stability of bodies?
Solution:
A rigid body can be in three equilibrium positions.
- a.) Stable position – after being displaced, the body returns to its original position
- b.) Neutral position – the body remains in the displaced position
- c.) Unstable position – the body does not return to its original position
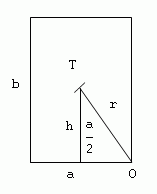
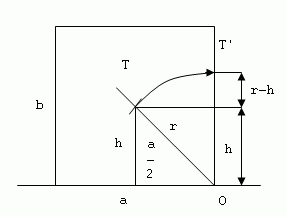The stability of a supported body is determined by the amount of work needed to overturn it from the stable to the unstable position.
W = m.g.(r – h)
m – mass of the body
h – distance of the center of gravity from the base in the upright position
r – distance of the center of gravity from the edge about which the body is overturned
r – h – elevation of the center of gravity during overturning
The stability of a body is high if it has a large mass and its center of gravity is as low as possible.
2.The dimensions of a brick are a = 0.3 m, b = 0.15 m, c = 0.06 m, and its mass is 5 kg. Calculate the work required to overturn the brick around edge b from the stable to the unstable position.
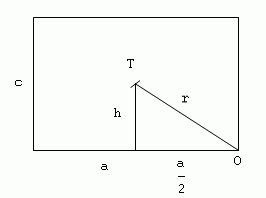
Solution:
Analysis:
a = 0.3 m, b = 0.15 m, c = 0.06 m, m = 5 kg,
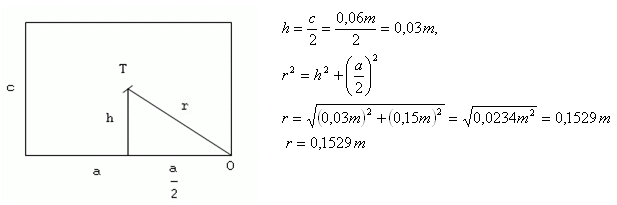
W = m.g.(r – h)
W = 5kg·10m·s-2·(0.1529m – 0.03m)
W = 50 kg·m·s-2·0.1229m = 6.145 J
W = 6.145 J
The work required to overturn the brick is W = 6.145 J.
3.What work is required to overturn a granite block (ρ = 2800 kg·m-3) in the shape of a cube with mass 1000 kg, over an edge, from one face to another?
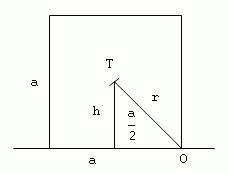
Solution:
Analysis:
m = 1000 kg, ρ = 2800 kg·m-3,
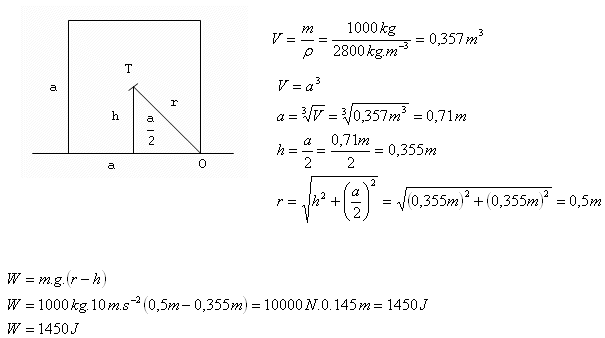
To overturn the granite block, the work required is W = 1450 J
4.A heavy brick block in the shape of a cuboid with height 2 m and width 1.5 m has a mass of 2500 kg. Compare the work required to overturn the block around the third edge according to the figures.
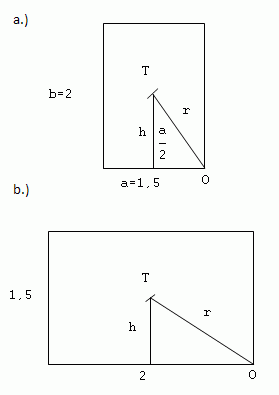
5.A granite square prism (ρ = 2500 kg·m-3) has a base edge of 60 cm and a height of 80 cm. What work must be done to overturn the prism from a stable equilibrium position to an unstable one? The prism is standing on a square base.
