Thermal expansion

1. Characterize the thermal expansion of solids, liquids, and gases!

Solution:

Thermal expansion is a change in an object's dimensions caused by a change in its temperature.

A.) Solids

1.) Linear expansion:

l=l0(1+α⋅Δt)l = l_0 (1 + \alpha \cdot \Delta t)

α\alpha = coefficient of thermal linear expansion

  • α(Cu)=1.7×10−5 K−1\alpha(\text{Cu}) = 1.7 \times 10^{-5} \, K^{-1}

  • α(Al)=2.4×10−5 K−1\alpha(\text{Al}) = 2.4 \times 10^{-5} \, K^{-1}

  • α(Fe)=1.2×10−5 K−1\alpha(\text{Fe}) = 1.2 \times 10^{-5} \, K^{-1}

Relative elongation:

ε=Δll0⋅100%\varepsilon = \frac{\Delta l}{l_0} \cdot 100 \%

2.) Volumetric expansion:

V=V0(1+3α⋅Δt)V = V_0 (1 + 3 \alpha \cdot \Delta t) ρ=ρ0(1−3α⋅Δt)\rho = \rho_0 (1 - 3 \alpha \cdot \Delta t)

B.) Liquids

Volumetric expansion:

V=V0(1+β⋅Δt)V = V_0 (1 + \beta \cdot \Delta t)

β\beta = coefficient of thermal volumetric expansion

  • β(H2O)=1.8×10−4 K−1\beta(\text{H}_2\text{O}) = 1.8 \times 10^{-4} \, K^{-1}

  • β(diesel)=1.1×10−3 K−1\beta(\text{diesel}) = 1.1 \times 10^{-3} \, K^{-1}

ρ=ρ0(1−β⋅Δt)\rho = \rho_0 (1 - \beta \cdot \Delta t)

C.) Gases

1.) Volumetric expansion:

V=V0(1+γ⋅Δt)V = V_0 (1 + \gamma \cdot \Delta t)

γ\gamma = coefficient of expansion is the same for all gases:

γ=1273.16 K=0.00366 K−1=3.66×10−3 K−1\gamma = \frac{1}{273.16 \, K} = 0.00366 \, K^{-1} = 3.66 \times 10^{-3} \, K^{-1}


2.A copper wire (α = 1,7.10-5K-1) had a length of 21,55 m at a temperature of -50C. What is its length at 300C? By how many cm did the wire lengthen?

Solution:

Analysis:

l0 = 21,55 m,  α = 1,7.10-5K-1 = 0,000017 K-1,  Δt = 300C - (-50C) = 350C

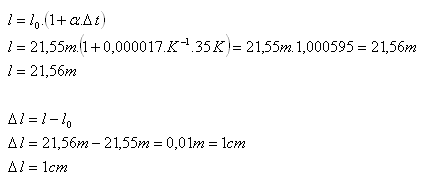
fyzika-tepelna-roztaznost-2.gif 

After heating, the wire has a length of 21,56 m. It lengthened by 1 cm.

3.A copper wire (α = 1,7.10-5K-1) whose length at 180C was 150 cm was heated by electric current and elongated by 9 mm. To what temperature was the wire heated?

Solution:

Analysis:

l0 = 150 cm = 1,5 m,   t1 = 180C,  Δl = 0,009 m,   α = 1,7.10-5K-1

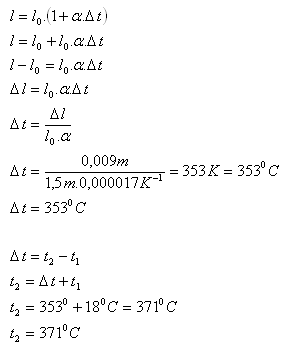
 fyzika-tepelna-roztaznost-3.gif

The wire was heated to a temperature of 3710C.

4.Two rods, one iron (α1 = 1,2.10-5K-1) and one zinc (α2 = 2,9.10-5K-1), had the same length at 00C. When their temperature is raised to 1000C, the difference in their lengths is 1 cm. What were their original lengths?

Please log in to view the solution.

5.An aluminum container (α (Al) = 24.10-6K-1) has an internal volume of 10 liters at 200C. How does its internal volume change at 1000C?

Please log in to view the solution.

6.Tables state that copper has a density of ρ20 = 8930 kg.m-3 at 200C. What is the density of copper at 800C?

Please log in to view the solution.

7.A floor tile is made of marble (α = 0,85.10-5K-1) and is square. The side of the tile has a length of 0,5 m at 00C. By how many cm2 does the area of the tile increase if its temperature is raised to 350C?

Please log in to view the solution.

8.A brass sphere (α = 1,8.10-1K-1) has a radius r1 = 2 cm at 150C. By how many 0C must it be heated so that it will no longer pass through a circular opening with radius r2 = 2,02 cm?

Please log in to view the solution.

9.A tank wagon is filled with diesel up to the opening. (ρ = 940 kg.m-3, β = 1.10-3K-1) At 00C the wagon holds 50 tons of diesel. How much diesel will spill out through the opening if the temperature of the diesel rises to 200C during the trip?

Please log in to view the solution.

10. The air in a vessel with a movable piston has a volume of 1 liter at 100C. What is the volume of the air at 400C? Also calculate the relative change in the volume of the air!

Please log in to view the solution.

11.A student named “Mistaken” claimed that from the relation l = l0(1 + αΔt) it follows that with sufficiently large cooling the length “l” of a rod will be zero. Could he be right? Which important law of nature does this claim contradict?

Please log in to view the solution.

12. A 200 m long heating pipeline was welded at a temperature of 200C. By how much will it lengthen if, under operating conditions, the temperature increases to 1200C?

Please log in to view the solution.

13.  At a temperature of 100C a copper cube has a volume of 600 cm3. How will its volume change when heated to 2100C?

Please log in to view the solution.

14.Calculate the coefficient of volumetric thermal expansion of gasoline, which has a volume of 10.3·10-3 m3 at a temperature of 300C and a volume of 10-2 m3 at a temperature of 00C.

Please log in to view the solution.

15. Calculate the mass of 1 dm3 of copper at a temperature of 4000C, given that at 00C the density of copper is 8.9·103 kg·m-3.

Please log in to view the solution.

16.At 00C a zinc rod has a length of 200 mm and a copper rod has a length of 201 mm. Their cross-sectional dimensions at 00C are the same. Calculate at what temperature the rods will have the same volume.

Please log in to view the solution.

17.A steel sphere has a radius of 2 cm at a temperature of 800C. What is the volume of this sphere at a temperature of –200C?

Please log in to view the solution.

18.How much heat is absorbed by a copper rod that has a length of 10 cm and a cross-section of 2 cm2 at 200C, if it lengthens by 0.1 mm when heated?

Please log in to view the solution.

19.A small ball oscillates on a thin steel wire with a period of 2 seconds. The length of the suspension at 200C is 2 meters. How does the period change if the pendulum is heated to 800C?

Please log in to view the solution.

20.By how much will an aluminum wire with a cross-section of 5 mm2 lengthen if an electric current with power 16 W passes through it for 1 minute? (Neglect heat losses)

Please log in to view the solution.