Pohyby v radiálnom gravitačnom poli
1. Charakterizujte radiálne gravitačné pole Zeme.
Riešenie:
Ak trajektória hmotného bodu pri pohybe v gravitačnom poli Zeme je porovnateľná s rozmermi Zeme, gravitačné pole je radiálne. Radiálne gravitačné pole je priestorovo neohraničené. Na rôznych miestach takéhoto poľa má gravitačné zrýchlenie rôzny smer, lebo stále smeruje do stredu Zeme a rozličnú veľkosť, ktorá závisí od vzdialenosti daného miesta od stredu Zeme. Príkladom pohybu v radiálne gravitačné pole Zeme sú pohyby umelých družíc Zeme, pohyby medzikontinentálnych striel a rakiet atď.
Na teleso o hmotnosti m pôsobí pri pohybe v gravitačnom poli Zeme
a) dostredivá sila: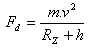
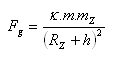
Teleso má
a) kinetickú energiu: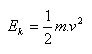
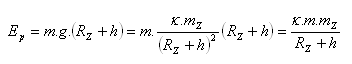
Pre radiálne gravitačné pole Slnka platia tri Keplerove zákony:
1.) Planéty sa pohybujú okolo Slnka po elipsách malo odlišných od kružníc, v spoločnom ohnisku je Slnko.2.) Plochy opísané sprievodičom planéty za rovnaký čas sú rovnaké.
3.)
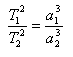T1, T2 sú obežné doby dvoch planét, a1, a2 sú hlavné polosi ich trajektórií.
2.Vypočítajte prvú a druhú kozmickú rýchlosť.
Riešenie:
- a.) Prvá kozmická rýchlosť v1
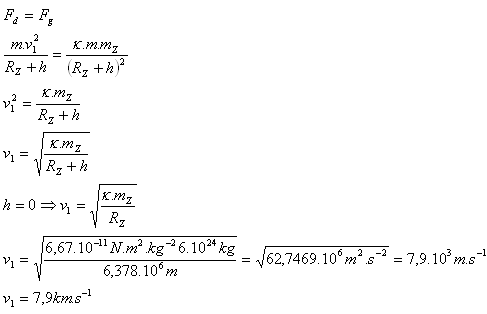
- b.) Druhá kozmická rýchlosť v2
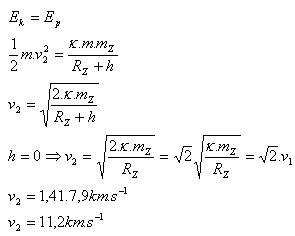
- Prvá kozmická rýchlosť (kruhová) je v1 =7,9 km.s-1.
- Druhá kozmická rýchlosť (parabolická, úniková) je v2 = 11,2 km.s-1.Teleso sa trvale vzďaľuje od Zeme ale zostáva v gravitačnom poli Slnka.
- Tretia kozmická rýchlosť je v3 = 16,7 km.s-1. Teleso opúšťa gravitačné pole Slnka.
3. V istej dobe boli zo Zeme pozorované dve družice v rôznych výškach (h1 = RZ, h2 = 2RZ), ktoré sa pohybovali po kruhových trajektóriách rovnakým smerom. Určite ich rýchlosti. v1 = 7,9 km.s-1
Riešenie:
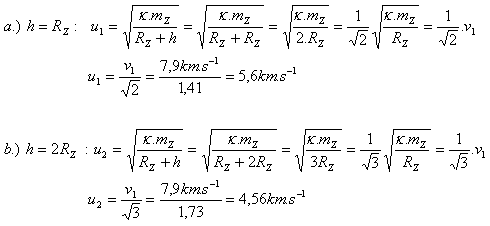
Rýchlosti družíc sú u1 = 5,6 km.s-1 a u2 = 4,56 km.s-1.
4.Určite parabolickú (druhú kozmickú) rýchlosť na povrchu Mesiaca. mM=7,41.1022 kg, RM=1,736.106 m
Prihláste sa pre zobrazenie riešenia
5. Hmotnosť Slnka je mS =1,989 1030 kg. Rýchlosť obehu Zeme okolo Slnka je v = 29,82 km.s-1. V akej vzdialenosti obieha Zem okolo Slnka?
Prihláste sa pre zobrazenie riešenia
6.Mesiac obieha okolo Zeme vo vzdialenosti 384 000 km a má hmotnosť 7,41.1022 kg. Na spojnici stredov obidvoch telies nájdite bod C, v ktorom by bol človek v beztiažovom stave. V tomto bode sa gravitačná sila Zeme rovná gravitačnej sile Mesiaca.
Prihláste sa pre zobrazenie riešenia
7.Najväčšia planéta Slnečnej sústavy Jupiter obieha okolo Slnka vo vzdialenosti 7,8.108 km. Hmotnosť Slnka je 1,989.1030 kg. Akú hmotnosť má Jupiter, ak ho Slnko priťahuje gravitačnou silou Fg= 4,2.1023 N? Aké veľké zrýchlenie udeľuje Slnko Jupiteru? Aký je obežný čas (perióda T) Jupitera okolo Slnka?
Prihláste sa pre zobrazenie riešenia
8.V akej výške h nad Zemou sa musí umiestniť stacionálna družica, ktorá sa nachádza nad tým istým miestom nad povrchom Zeme?
Prihláste sa pre zobrazenie riešenia
9. Pomocou Keplerových zákonov zistite:
- a.) Aká je stredná vzdialenosť planéty Venuša od Slnka, ak jej doba obehu okolo Slnka je
TV=0,615 roka. - b.) Aké je doba obehu planéty Merkúr okolo Slnka, ak jej stredná vzdialenosť od Slnka je
aM = 0,387AU
10.Kozmická loď štartuje zo stacionárnej obežnej stanice umiestnenej vo výške h = 35 856 km nad Zemou (viď príkl. č.8) smerom na Mesiac. Za aký čas sa kozmická loď dostane do oblasti Mesiaca?
Prihláste sa pre zobrazenie riešenia
