Binomická veta
1. Napíše binomickú vetu a jej vlastnosti:
Binomická veta a Pascalov trojuhoník.
Binomická veta
Pre ľubovoľné a, b є R, n є N platí:
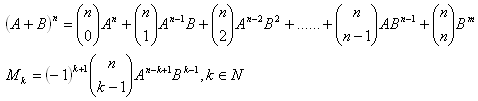
Pascalov trojuholník
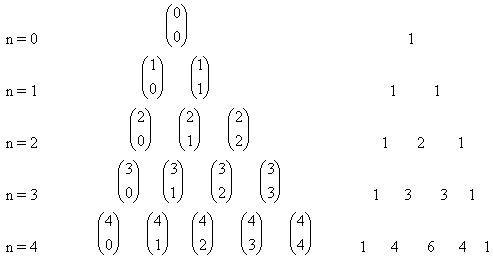
Platí:
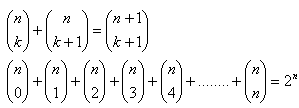
Pre ľubovoľné a, b є R, n є N platí:
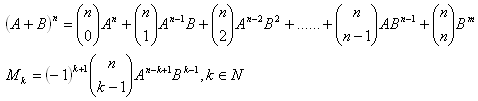
Pascalov trojuholník
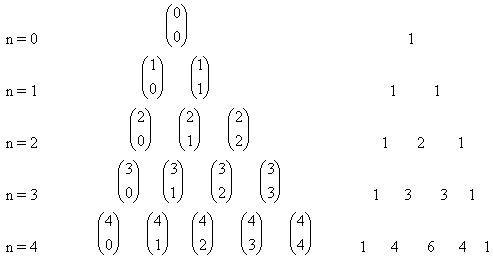
Platí:
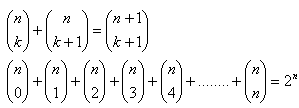
2. Zjednodušte:
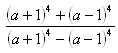
Riešenie:
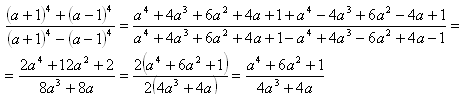
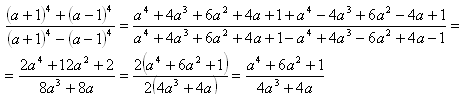
3. Zjednodušte:
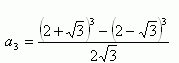
Riešenie:
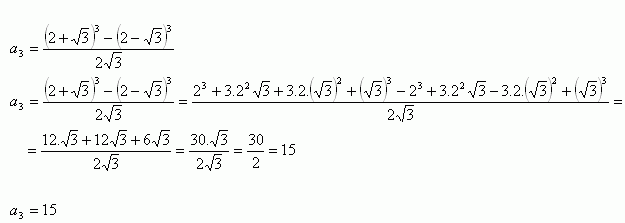
4. Určite štvrtý člen binomického rozvoja:
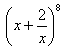
5. Určite člen binomického rozvoja ( x + x-1)8, ktorý neobsahuje x.
Prihláste sa pre zobrazenie riešenia6. Ktorý člen rozvoja (2x3 + x–1)10 obsahuje x6.
Prihláste sa pre zobrazenie riešenia7. V rozvoji (a + 2a3)n je koeficient 3. člena o 44 väčší ako koeficient 2. člena.
Určite, pre ktoré prirodzené číslo platia uvedené podmienky.
8. Pre ktoré x sa v rozvoji výrazu rovná M5 = 105?
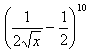
9.
Zistite ktorý člen daného rozvoja obsahuje x7, ak platí:
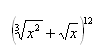
10. Nájdite najväčší koeficient binomického rozvoja (a + b)n, keď súčet všetkých koeficientov je 4096.
Prihláste sa pre zobrazenie riešenia