Dve priamky v rovine
1. Charakterizujte vlastnosti dvoch priamok v rovine.
Dve priamky p, q v rovine sú:
a) rovnobežné rôzne
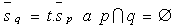
b) rovnobežné totožné
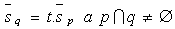
c) rôznobežné
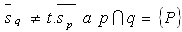
Priesečník dvoch rôznobežných priamok P sa určí riešením sústavy ich rovníc.
Uhol dvoch priamok φ sa určí ako uhol ich smerových (normálových) vektorov alebo pomocou ich smerníc kp, kq
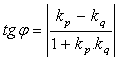
Vzdialenosť dvoch rovnobežných priamok d sa určí ako vzdialenosť bodu (ktorý patrí jednej priamke), od druhej priamky.
Os uhla dvoch rôznobežných priamok je priamka, ktorej body majú rovnakú vzdialenosť od obidvoch rôznobežiek. (dp = dq)
2. Zistite vzájomnú polohu priamok p a q, ak platí:
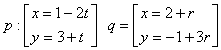
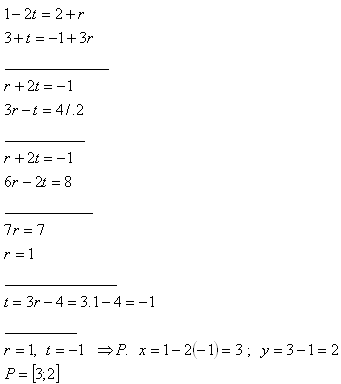
Priamky p, q sú rôznobežné a pretínajú sa v bode P[3;2].
3. Zistite vzájomnú polohu priamok p a q, ak platí:
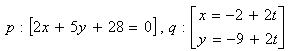
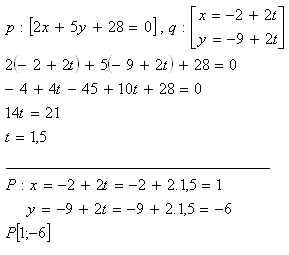
Priamky sú rôznobežné a pretínajú sa v bode P[1;-6].
4. Rovnice strán trojuholníka Δ ABC sú:
b: [2x + 7y – 70 = 0]
c: [7x + 2y -20 = 0]
Vypočítajte vrcholy tohto trojuholníka.
5. Protiľahlé strany štvorca ležia na rovnobežných priamkach:
q: [5x - 12y + 26 = 0]
Zistite obsah štvorca.
6. Trojuholník ΔABC je daný stranami:
b: [x – y – 3 = 0]
c: [x – 2y + 3 = 0]
Určite:
a) vrcholy trojuholníka
b) stred a polomer kružnice trojuholníku opísanej
7. K bodu M [1;2] zistite bod N [x;y], ktorý je symetrický s priamkou p:[x – y - 1 = 0].
Prihláste sa pre zobrazenie riešenia8. Napíšte rovnicu osi uhla priamok:
q: [5x – 12y + 26 = 0]
9. Napíšte rovnicu priamky q, ktorá prechádza bodom M [1;3] a zviera s priamkou p :[ 2x – y + 5 = 0] uhol φ = 45°.
Prihláste sa pre zobrazenie riešenia10. Tri susedné dediny majú na pláne túto polohu:
B[5;-2]
C[10;3]
V ktorom mieste bude umiestnený spoločný kultúrny dom, ku ktorému má byť zo všetkých troch dedín rovnako ďaleko?
11. Nájdite množinu všetkých bodov v rovine, ktoré majú rovnaké vzdialenosti od rovnobežiek:
q: [4x – 6y + 5 = 0]
12. Na priamke p: [5x – 4y - 28 = 0] určite bod, ktorý má od bodov M [1;5] a N [7;-3] rovnakú vzdialenosť.
Prihláste sa pre zobrazenie riešenia13. Určite súradnice stredu štvorca ABCD, ak je daný jeho vrchol A[-3;-4] a uhlopriečka BD leží na priamke p: [3x +4y – 25 = 0].
14. Určite geometrické miesto bodov, ktorých vzdialenosti od priamok:
q: [12x – 5y – 13 = 0]
sú v pomere dp:dq = 2:3.