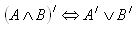Výroky
1.Charakterizujte základné vlastnosti výrokov.
Riešenie:
Výrok je každá oznamovacia veta, o ktorej má zmysel uvažovať či je pravdivá alebo nepravdivá. Výroky označujeme: A, B, C, D, V, ... atď.
Výrok
- a) pravdivý - „platí“ má pravdivostnú hodnotu (1)
- b) nepravdivý – „neplatí“ má pravdivostnú hodnotu (0)
Negácia výroku
Ku každému výroku A možno vytvoriť výrok A‘, ktorý popiera (neguje) to , čo tvrdí výrok A. Výrok A‘ sa nazýva negácia výroku A. Negáciu vytvoríme tak, že pred výrok dáme predponu „ne ..“, „nie je“, alebo text „nie je pravda že ....“.
| A | A‘ |
| (1) | (0) |
| (0) | (1) |
2.K daným výrokom vytvorte ich negácie. Určite pravdivostné hodnoty pôvodných a negovaných výrokov.
A: Číslo 3 je prvočíslo (1)
B: Bratislava leží v Egypte (0)
C: Prešovský kraj
D: Matematika je veda (1)
E: Číslo 22 je deliteľné 2 (1)
F: Dobrý deň !
G: Existuje snežný muž Yetti
H: Sínus 300 je – 2,1 (0)
I: Máš domácu úlohu?
J: x2 -5x +6 = 0
K: Číslo 2574364 je deliteľné 4 (1)
L: Platí že (a + b)2 = a2 + b2 (0)
M: Obsah kruhu je S = π.r2 (1)
N: 42 sa rovná 18 (0)rovná 18 (1)
O: Mám nové auto (1)
P: Nie je tu.
Riešenie:
A': Číslo 3 nie je prvočíslo (0)
B': Bratislava neleží v Egypte (1)
C : nie je výrok
D': Matematika nie je veda (0)
E': Číslo 22 nie je deliteľné 2 (0)
F : nie je výrok
G : nedá sa rozhodnúť
H': Sínus 300 nie je -2,1 (1)
I : nie je výrok
J : nie je výrok
K': Číslo 2574364 nie je deliteľné 4 (0)
L': Neplatí že ( a + b )2 = a2 + b2 (1)
M': Obsah kruhu nie je S = π.r2 (0)
N': Nie je pravda, že 42 sa rovná 18 (1)
O': Nemám nové auto (0)
P : nie je výrok
3.Zopakujme si vlastnosti kvantifikovaného výroku.
Riešenie:
Kvantifikovaný výrok je oznamovacia veta, ktorá udáva určitý počet,alebo odhad počtu predmetov, osôb atď. s rovnakou vlastnosťou. V kvantifikovanom výroku sa vyskytujú slová: práve, najviac, každý, všetci, niektorí, aspoň, žiadny ...atď., ktoré sa nazývajú kvantifikátory a číslovky.
- Výrok „aspoň 5“ znamená 5 a viac.
- Výrok „najviac 5“ znamená 5 a menej
Pre symbolické zápisy kvantifikovaných výrokov používame
- a) všeobecný kvantifikátor
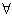 - „pre každé (všetky) platí.....“
- „pre každé (všetky) platí.....“ - b) existenčný kvantifikátor
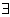 - „existuje aspoň jedno..., pre ktoré platí ....“
- „existuje aspoň jedno..., pre ktoré platí ....“
Negácia kvantifikovaného výroku
| Výrok | Negácia výroku |
| Každý ... je ... | Aspoň jeden... nie je ... |
| Aspoň jeden ... je ... | Každý ... nie je ... |
| Aspoň n ... je ...(n>1) | Najviac (n-1)... je ... |
| Najviac n ... je ... (n>=1) | Aspoň (n+1)... je ... |
| Práve n ... je ... | Najviac (n-1) alebo aspoň (n+1) je... |
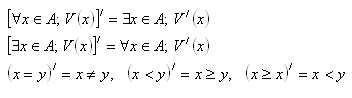
4. Negujte nasledujúce výroky:
A: Číslo 3 je koreňom rovnice x2 = 9 (1)
B : 23 -5 > 7 (0)
C: Uhlopriečky štvorca sú na seba kolmé (1)
D: 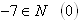
E: Každá úloha má riešenie (0)
F: Existuje aspoň jeden obdĺžnik, ktorý má kolmé uhlopriečky (0)
G: Existuje aspoň jeden pravouhlý trojuholník (1)
H: Táto kniha má najviac 50 strán (1)
I: Každá pieseň má koniec (1)
J: Na zasadnutí ZRPŠ bolo práve 20 rodičov (0)
K: 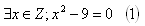
L: 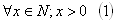
5. Čo vieme o zložených výrokoch?
Prihláste sa pre zobrazenie riešenia
6.Negujte nasledujúce výroky:
A: Príde Peter a Mária
B: Prší a je mokro
C: Svieti slnko alebo fúka vietor
D: Ak sa nahneváme, budeme zlí
E: Ak príde Jozef, potom príde aj Eva
F: Mám dobrú náladu práve vtedy, keď prší
G: Každý lichobežník je rovnostranný
H: Existuje aspoň jedno prvočíslo, ktoré je párne
I: V triede 1.A aspoň 8 žiakov nosí okuliare
J: 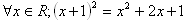
7. Z daných výrokov A, B vytvorte:
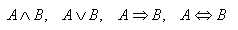
8.Dané sú výroky P: prší , S: svieti Slnko, V: fúka vietor. Vytvorte z nich zložené výroky
Prihláste sa pre zobrazenie riešenia
9.Zistite pomocou tabuľky pravdivostnú hodnotu formuly: