Trojuholník
1.Charakterizujte obecný trojuholník
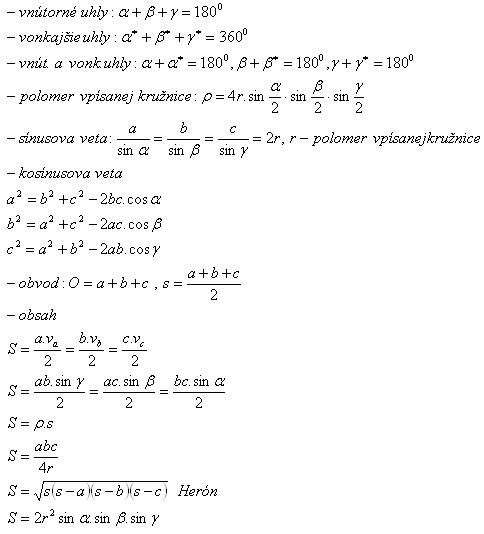
2. Dokážte, že pre vonkajšie uhly trojuholníka platí α*+ β*+ γ* = 360°.
α + α* = 180°
β + β* = 180°
γ + γ* = 180°
_____________
α + β + γ + α* + β* + γ* = 540°
α* + β* + γ* = 540° – (α + β + γ)
α* + β* + γ* = 540° - 180°
α* + β* + γ* = 360°
3. Trojuholník má stranu c = 40 cm. Pre jeho uhly platí: α:β:γ = 3:5:10.
a) obvod
b) obsah
Obvod
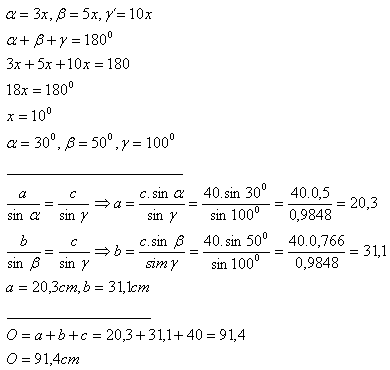
Obsah
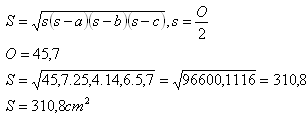
4. Daný je rovnostranný trojuholník so stranou a = 10 cm.
5. Janko je od jedného konca stromu padnutého na zem vzdialený 5 m, od druhého 8m. Strom vidí pod zorným uhlom 60°.
6. Tri kružnice s polomermi r1 = 2 cm, r2 = 3cm, r3 = 4cm majú vonkajší dotyk.
7. Zo stanice súčasne vyšli dva vlaky na priamych tratiach, zvierajúcich uhol φ = 156°
rýchlosťami v1 = 13 ms-1, v2 = 14,5 ms-1.
8. Sily F1, F2 majú spoločné pôsobisko a zvierajú uhol φ = 60°.
- Aká veľká je ich výslednica, ak F1 = 42N, F2 = 35N.
- Určite uhly, ktoré zvierajú sily F1, F2 s výslednicou.
9. Z veže vysokej 20 m a vzdialenej od rieky 20 m sa javí šírka rieky pod uhlom 15°.
10. Teleso, ktoré má hmotnosť m = 1563 kg je zavesené na vodorovnom tráme na dvoch lanách rôznej dĺžky. Laná zvierajú s trámom uhly α = 48°, β = 62°.