Kvadratúra
1.Vysvetlite pojem „kvadratúra“
Riešenie:
Kvadratúra je výpočet obsahu rovinného útvaru, ktorý je ohraničený osou x , dvoma rovnobežkami s osou y v bodoch x1 = a, x2 = b a čiarou ( priamkou alebo krivkou ), ktorá má rovnicu y = f(x).
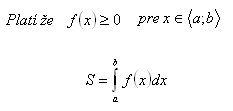
2.Pomocou určitého integrálu odvoďte vzorec pre výpočet obsahu
- a) štvorca
- b) obdĺžnika
Riešenie:
a) Štvorec
Štvorec je ohraničený osou x, priamkou y = a a priamkami rovnobežnými s osou y v bodoch a = 0, b = a.
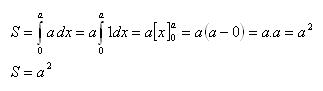
b) Obdĺžnik
Obdĺžnik je ohraničený osou x , priamkou y = b a priamkami rovnobežnými s osou y v bodoch a=0, b=a.
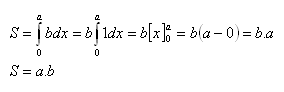
3.Pomocou určitého integrálu odvoďte vzorec pre výpočet obsahu
- a) rovnoramenného trojuholníka
- b) rovnoramenného lichobežníka
Riešenie:
a) Rovnoramenný trojuholník
Rovnoramenný trojuholník má základňu a, výšku v. Nech S1 je polovičný obsah tohto trojuholníka, ktorý je ohraničený osou x, priamkami rovnobežnými s osou y v bodoch a = 0, b = v a priamkou
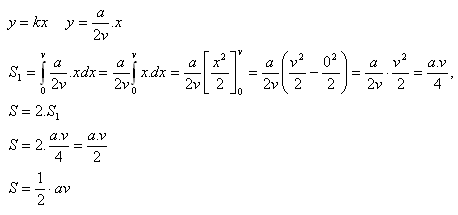
b) Rovnoramenný lichobežník
Rovnoramenný lichobežník má hornú základňu a, dolnú b a výšku v. Nech S1 je polovičný obsah tohto lichobežníka, ktorý je ohraničený osou x, priamkami rovnobežnými s osou y v bodoch a = 0, b = v a priamkou
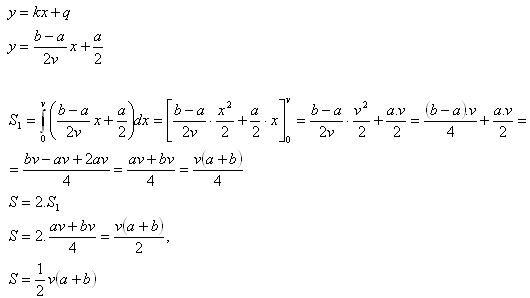
4.Vypočítajte obsah útvaru ohraničeného parabolou y = x2 + 1 a priamkou y = 5.
Prihláste sa pre zobrazenie riešenia
5.Pomocou určitého integrálu vypočítajte obsah rovinného útvaru ohraničeného parabolami
y = 6 – 4x + x2 a y = –3 + 8x –2x2.
Prihláste sa pre zobrazenie riešenia
6. Odvoďte vzorec pre výpočet obsahu kruhu s polomerom r.
Prihláste sa pre zobrazenie riešenia
7.Odvoďte vzorec pre obsah elipsy, ktorej poloosi sú „a“ a „b“.
Prihláste sa pre zobrazenie riešenia